Statistical Inference: Simulation
Although it is possible that the yawn seed doesn't help and the researchers were just lucky and happened to assign more of the subjects who were going to yawn anyway into the yawn seed group, the key question is whether this explanation is plausible.
Terminology detour: The "by chance" hypothesis that we have been using as the basis of our simulations is more typically known as the "null hypothesis." In general, the null hypothesis usually makes some uninteresting or "dull" claim about the population or process. Here the claim is that the yawn seen treatment has no effect on the likelihood of someone yawning. Or in other words, that the probability of yawning is the same for both treatment groups. On the other hand, the other possibility, what we are actually hoping to show is called the "alternative hypothesis." In Lab 1, this was that infants are more likely to choose the friendly toy. would be on the left more often. Here, we suspect the yawn seed helps, so the alternative hypothesis is that the probability of yawning is higher for the yawn seed treatment than for the control group |
So as before, we will assume our null hypothesis is true, and decide whether we have convincing evidence in favor of our alternative hypothesis (if our data is too unlikely to occur by chance alone when the null hypothesis is true). So what do we mean by "chance alone" in this research study?
We want, as in Lab 1, to hypothetically replicate the study but where we know the null hypothesis is true to see what kind of "chance variation" there is the sample results. For this lab, instead of imitating the process of randomly choosing (as in Lab 1) we need to simulate the random assignment process under the scenario where there is no effect from the yawn seed. To do this, we will suppose we were going to have 14 “yawners” and 36 non-yawners no matter which treatment group they ended up in, and we’ll randomly assign 34 of these 50 subjects to the yawn seed group and the remaining 16 to the control group.
So now the practical question is, how do we do this hypothetical random assignment? One answer is to use cards:
- Take a set of 50 index cards with 14 blue cards (to represent the yawners) and 36 green cards (to represent those that didn't yawn). (Alternatively you could use playing cards with red suits and black suits or face cards and non-face cards.)
- Shuffle the cards well and randomly deal out 34 to be the yawn seed group (the rest are the control/no yawn seed group).
- Count how many yawners (blue cards) you have in each group and how many non-yawners (green cards) you have in each group.
- Construct the two-way table to show the number of yawners and non-yawners in each group (where clearly nothing different happened to those in “group A” and those in “group B” – any differences between the two groups that arise are due purely to the chance inherent random assignment process).
Here are the results of one such "could have been" random assignment. Notice that of the 34 cards in the seeded group, some came from the seeded group originally (with the dark blue band) and some did not.
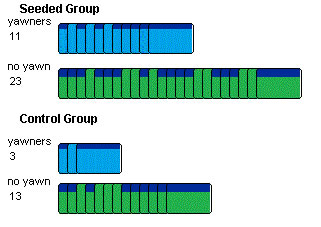
The results of this random assignment can be put into a two-way table.
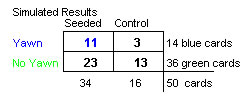
(e) Compute the difference in the conditional proportion of yawners in each treatment group.
(f) How does this hypothetical result compare to the difference that the Mythbusters found? Which difference (yours or theirs) provides more evidence that the yawn seed is effective? (If our "could have been" results, which arose solely by random chance, does, then we are starting to think their result is a little less impressive... )

