Theory-Based Inference
When the sample size conditions for the Central Limit Theorem are met, we can use the Theory-Based Inference applet to obtain a p-value. (There are some technical details in how the computer performs these calculations but we will ignore that for now.)
- In the JMP output window, use the red arrow next to Sleep Hrs to pull down the menu.
- Select Test Mean.
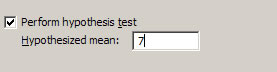
- Specify our Hypothesized Mean. Press OK. (We are not assuming we know the population standard deviation.)
|  |
- Use the pull-down menu from the SleepHrs box and select Confidence Interval > 0.95.
- Focus on the Lower CI value and the Upper CI value in the first row (for the mean).
- Copy and paste the resulting Test Mean and Confidence Intervals output into your report
|  |
Copy and paste this output into your report.
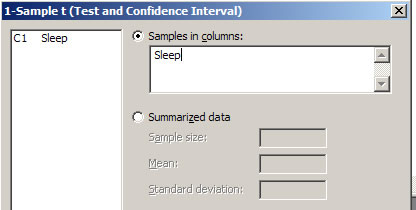
- Again select Stat > Basic Statistics > 1-Sample t.
- The sleep data should still be in the Samples in columns box.
- You can unselect the Perform hypothesis test box,
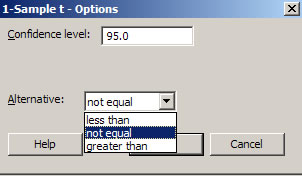
- but click Options and make sure the Confidence level is set to 95.0 and the Alternative is set to "not equal."
|
 |
Copy and paste this output into your report.
Theory Based Inference applet
- Use the pull-down menu to change from One proportion to One mean.
- Check the Paste Data box and the Include header boxes.
- Again, copy and paste the data for all of column A into the Sample Data box (or type in the summary statistics) and press Use Data.
- Check the box for the Test of Significance.
- Specify the hypothesized value of the mean and if necessary press the button on the second line to toggle the direction of the alternative hypothesis.
- Press Calculate.
- Include a screen capture of your input and output in your report.
Note: The standardized statistic is now called a "t-statistic." We will see why next week.
(p) Report the relevant p-value. How does this p-value compare to what you found in the simulations? Provide an interpretation of this p-value in this context. (It's the percentage of what's that do what assuming what?)
(q) Based on this p-value (and the standard cut-off values from Lab 1), will you reject or fail to reject the null hypothesis?