Stat 301 – Exam 1 Preparations

Review Problems: Review problems (solutions)

See also: Examples 1.1 and 1.3, Chapter 1 Summary, ISCAM Glossary, the salmon-colored boxes and Chapter 1 Summary and Choice of Procedures table. There are also a few “practice quizzes” and “What went wrong”? questions in Canvas.

Required by midnight Wednesday: Submit Review 1 questions (parts 1 and 2) in Canvas discussion boards

Is there interest in a zoom review session Thursday evening?

Exam Format: The exam will cover topics from Investigation A, Investigation B, and Chapter 1 (HW 1-3, not Inv 1.7 or Inv 1.11). The exam questions will be mostly short-answer questions, often with several questions on the same study (but you do not necessarily have to answer (a) to try (b) etc.). You may use one page of your own notes (8.5 x 11, front and back). See formulas below?

You will not be expected to use R/JMP/applets but to read output (from any of these) and/or to use your calculator and/or to set up calculations by hand (show the values substituted into the formula). You will be expected to explain your reasoning, indicate your steps, and interpret your results. The exam will be worth approximately 50 points, so plan to spend one minute per point.

Study Advice: You should study from the text (including study conclusions, chapter examples, and chapter summary), powerpoints (in Canvas, see Schedule View), graded homeworks, hw solutions (follow original HW submission link), and graded practice questions. The quiz questions/solutions (and added commentaries) should be accessible to you in Canvas. In studying, I recommend going back through investigations, practice questions, and homeworks, without looking at the solutions, then check your answers, then repeat. (If you want solutions to the Practice Problems in the text, let me know.)

Overview: The exam will focus on studies that involve one binary categorical (i.e., yes/no) variable, where the data are a sample of independent (repeat) observations from a random process (the randomness is in the outcome) or a random sample from a large population (the randomness is in which observational units are in your sample). We have touched on descriptive statistics (e.g., count vs. percentage vs. proportion, bar graphs with “active” titles) and have studied two main types of statistical inference:

• Statistical significance, where the goal is to assess the degree to which the sample data provide evidence against a null hypothesis and in support of a research conjecture (alternative hypothesis);

• Statistical confidence, where the goal is to estimate a population parameter with an interval of plausible values.

Big Idea: We have a categorical variable and we have gathered observations from a random process or a random sample from a larger population. From that sample, we want to infer something about the underlying process or population. In other words, we want to use the statistic (which we calculate from our sample data) to test claims about (test of significance) or to estimate (confidence interval) the value of the parameter (which we don’t know). To do this, we need to assess the amount of “random variation” in our statistic, how much the statistic varies from sample to sample by chance alone. We can use simulation or the binomial distribution or (often) the normal distribution to predict what that variation in the statistic looks like. If our model of that randomness is appropriate, then we know how far the statistic might vary randomly from the parameter “by chance alone.”

From Investigation A you should be able to:

· Critique and suggest suitable comparisons to answer a research question

· Describe the sample distribution of a quantitative variable (shape, center, variability, outliers)

o Interpret the mean and standard deviation of a data set in context

o Interpret a histogram of a quantitative variable (e.g., skewed right vs. skewed left)

o Remember to talk in terms of distribution not just individual values

· Anticipate and explain variable behavior including outliers

o E.g., why might it make sense for a distribution to be skewed to the right?

From Investigation B you should be able to:

· Interpret probability as a long-run proportion (under identical conditions)

· Interpret expected value as a long-run average

· Use simulation to estimate a probability

· Distinguish between “exact” probability calculations and simulated results

From Section 1.1 (Inv 1.1-1.6) you should be able to:

· Define the observational units and variable of interest in a study

· Classify the variable as quantitative or categorical

· Produce a bar graph to summarize the sample distribution of a categorical variable

· Calculate a statistic to summarize a binary variable (e.g., sample count, X, or sample proportion, )

· Define a corresponding parameter of interest in the study in words (e.g., process probability or population proportion)

· Use appropriate symbols to refer to parameters and statistics

· Describe how to carry out a tactile simulation to represent a “random choice” process (e.g., with a coin or a die or a spinner) and to estimate a p-value

· Describe and interpret the results of a simulation

· Describe the sampling or null distribution in context

· Describe how to use the One Proportion Inference applet to set up a simulation given a null and alternative hypothesis, sample result

· Use the output from the One Proportion Inference applet to find a simulation-based p-value

· Set up a binomial probability calculation given values for n and (show numbers plugged into equation, use P(X > k) notation)

· Distinguish between the “simulation-based” and “exact” p-values

· Provide a “layman’s” interpretation of p-value in your own words in the context of the research question

· Explain what is meant by “statistical significance” and how it is assessed

· Don’t use the term “significant” in this course unless you are referencing a p-value

· Draw a conclusion about the “random chance” hypothesis based on a p-value

· State null and alternative hypothesis in symbols and in words (including choosing less than, greater than, or not equal to for the alternative)

· Predict the behavior of the binomial distribution of counts (e.g., skewed vs. symmetric, center)

· Same behavior as the distribution of sample proportions (but theoretical formulas change)

· Refer to this as the sampling or null distribution

· Carry out a binomial test of significance

· Define parameter

· State hypotheses (one or two-sided)

· Use a graph of the binomial distribution to estimate the p-value (one or two-sided)

· Make a decision to reject or fail to reject the null hypothesis based on the magnitude of the p-value

· Make a final conclusion in context about the research question

· Interpret a confidence interval as a range of plausible values for the parameter (those not rejected by a two-sided test)

· Recognize output for a binomial confidence interval

· Interpret a confidence interval in context, including a statement of the reliability of the method (the confidence level)

· Understand that the level of significance controls the probability of rejecting the null hypothesis when the null hypothesis is true (aka Type I Error)

· The rejection region is the values of the statistic that would lead you to reject the null hypothesis.

· Determine the probability of rejecting the null hypothesis for an alternative value of the parameter

· E.g., how often will a .333 hitter convince the manager is better than a .250 hitter (has to get 9 hits to be convincing, how often will a .333 hitter do so)

· Aka the power of the rest

· Visual

· Identify the factors that affect power and how

· Understand idea of using technology to determine the sample size necessary to achieve a stated power for a particular value of the alternative

From Section 1.2 (Inv 1.8-1.10) you should be able to:

· Determine whether or not the normal approximation to the binomial distribution (aka the CLT) is reasonable (show details) for the (null or sampling) distribution of the sample proportion (be able to sketch, scale, and label the predicted distribution)

o Remember this is a separate module on the normal distribution for a quantitative variable for additional practice

· Determine the mean and standard deviation for the distribution of the sample proportion

o Apply the CLT to predict the shape of a sampling distribution, including drawing a well-labeled and partially scaled (3-5 values on the horizontal axis) sketch of the distribution and shade the area of interest

o Consider probabilities as areas under a continuous mathematical probability curve

· Calculate and interpret the standardized statistic (aka z-score) for a sample proportion (using the theoretical mean and standard deviation of the distribution of sample proportions)

· Carry out a one-proportion z-test of significance

1. Define parameter

2. State hypotheses (one or two-sided)

3. Be able to calculate and interpret the test statistic (aka standardized statistic)

4. Check whether the (“theory-based” procedure is valid for the sample size used

§ It’s really converting the z-value to a p-value that requires the large sample size

5. Use a graph of the normal distribution to approximate a p-value (one or two-sided)

§ Be able to interpret applet, R, JMP output

6. Make a decision to reject or fail to reject the null hypothesis based on the magnitude of the p-value

7. Make a final conclusion in context about the research question

· Distinguish between the theory-based (normal distribution) and exact (binomial distribution) p-values.

· Apply and explain the logic behind a continuity correction for the p-value

· Calculate power using the normal distribution for a given alternative value

· Solve for the sample size necessary to achieve a certain level of power

· Calculate/Show how to calculate a one-sample z-confidence interval

· Interpret output of a one-sample z-confidence interval

· Explain the components of the confidence interval formula (e.g., midpoint, width)

· Determine and interpret margin-of-error as the measured of expected random (sampling) error

· Identify the factors that affect the midpoint and width of the confidence interval

· Solve for the sample size necessary to achieve a desired margin of error (See Inv 1.9(m))

· Interpret confidence level in terms of the reliability of the method

· Describe impact of changing the confidence level on the interval

· Apply and explain the Plus Four (aka adjusted Wald) procedure for 95% confidence

· Identify Wald vs. Plus Four vs. Binomial and when they will be similar

· Never a bad idea to use “plus four”

· Describe and utilize the duality between two-sided tests and confidence intervals

From Section 1.3 (Inv 1.12-1.18) you should be able to:

· Define the population, sample, sampling frame, statistic, and parameter for a particular study context

· Decide whether a sampling method is unbiased by

· Examining the sampling distribution of the statistic, and determining whether it is (approximately) centered at the population parameter value

· Considering whether the sampling frame is complete and whether the selection method is random, based on a description of the sampling process.

· Be able to conjecture with justification a direction for sampling or nonsampling bias (describe whether likely to systematically produce over or underestimates of the parameter value and why)

· Know the difference between “bias” and an unlucky sample

· Produce a simple random sample from a sampling frame, e.g., with GRN applet, Random.org

· Describe the concept of (random) sampling variability to a nonstatistician

· Identify the following sampling methods from a description: systematic sampling, multistage sampling, stratified sampling

· Explain how they differ from a simple random sample

· Suggest sampling and nonsampling errors present in a study context (see Investigation 1.15; Example 1.3)

· Describe the difference between statistical significance and practical significance (Investigation 1.17)

· Realize that when we are sampling from a finite population, the binomial distribution is an approximation

· This approximation is more valid the larger the population size compared to the sample size (e.g., N > 20n)

· The hypergeometric distribution (and related ‘finite population correlation factor’ will not be covered on Exam 1. Instead we will work with very large populations and use the binomial approximation and/or the normal approximation to the hypergeometric.

· When this approximation is valid, we apply all the same techniques (e.g., simulation, binomial, normal) as earlier in the chapter.

· When this approximation is valid, neither the population size nor the percentage of the population sampled influence our statements of significance or confidence

Which distribution do I use to find a p-value or a confidence interval?

· You have several options for categorical data (assuming you are sampling a binary variable from a random process or a large population)

o Simulation, although don’t have confidence interval or power formulas

o The binomial distribution, although don’t have confidence interval or power formulas (referred to as exact procedures)

o The normal distribution if the conditions for the CLT are met (referred to as z-procedures)

Miscellaneous

• Be able to define a probability as a long-run proportion (e.g., whether it’s a probability from a model, from a normal distribution, from a p-value)

o What is the random process being repeated, what is the outcome of interest

• Clearly differentiate parameters from statistics (e.g., parameter = long-run proportion or proportion of all adults)

o Probably not “past tense” (not observed)

• Don’t mix counts, proportions, percentages

• Be able to state hypotheses in symbols and/or words

o Use symbols correctly (e.g., know when you are using and when or )

• Clearly explain how you are finding your output (e.g., which command used)

• Choice of success is often arbitrary, just make sure you are consistent

o Specifying one outcome as success doesn’t mean you have to use a one-sided alternative

• Thinking about your sample size can often help you define the observational units

• Be able to define what each dot represents and the variable in our “null” distributions (aka sampling distributions) vs. the sample distribution

• A calculation will seldom be the end of the question – always be on the look out for “and interpret”

• We can now give better answers to some of the early “generalizability” questions

• Always put your comments in context

• Be able to sketch and label the predicted null distribution

• Know the difference between “simulated” and “theoretical” values (e.g., for mean and SD, p-value)

• Some interesting results that we didn’t really derive but can certainly use

o SD() maximized at = .5

o Sample size effects are larger than effects on SD() but exhibit diminishing returns

o 1/ is pretty good approximation of margin-of-error for 95% confidence for .

• It’s possible I will say find the p-value or interval and if normal approximation is not valid you should not use it

o Remember the sample size checks differ slightly between a test and an interval

o For proportions: Binomial and Plus Four (95%) can be used with any sample size

• Be able to explain what is meant by “95% confidence” in your own words, in context, without using the words confidence, probability, sure, or chance

• Be able to interpret a p-value in your own words, not only evaluate

• Know the factors that affect test statistic, p-value, confidence intervals, and power/types of error probabilities

• Be able to suggest a continuity correction (for tail probabilities, “outside” and “between”; counts and/or proportions)

• Keep in mind we never get evidence for the null, only lack of evidence against it

o Absence of evidence is not evidence of absence

• When making a choice between two options, you should argue both for one and against the other (sometimes you tell me one has one property/advantage but don’t really tell me why the other does not)

o Make sure your explanations/justifications aren’t too “circular” (e.g., I have a larger confidence level because I am more certain the parameter is contained in the interval)

• Be able to evaluate the appropriateness of a model, understand the assumptions underlying a model

o e.g., how to check the four conditions of a binomial model (e.g., is it ok to assume the infants’ choices are independent of each other?)

o e.g., how to also check the sample size conditions for a normal approximation to the binomial

o e.g., how to check the population size conditions for the binomial approximation when sampling from a finite population

• You won’t do a lot of hand calculations but may be asked to set up an equation (e.g., pick the right expression with the values substituted in) or explain a property using the equation (e.g., because n is in the denominator)

• We don’t always want to assume 0.5 in Ho/Ha. The choices of hypothesized value and alternative direction are based entirely on the research question, not anything about the observed sample data.

o Match the direction of the alternative hypothesis to a stated research question

• If confidence level is stated, use 95%. If no significance level is stated, you can use 5%. Don’t interchange the phrases “significance” and “confidence”

Advice:

• Part of your grade will be based on communication. Be precise in your statements and use of terminology. Avoid unclear statements, and especially don’t use the word “it”! Always relate your comments to the study context.

o I would also avoid “data,” “results,” “accurate” because I don’t usually know what you mean by them

o Also say the distribution of what and the standard deviation of what

• Show the details of any of your calculations (including sample size checks)

• Organize notes for efficient retrieval of information/formulas

• Don’t plan to use your notes too much

o Prepare as if exam were closed book/notes

o Focus on understanding, not memorization

o Be cognizant of time constraint

• Expect similar questions to what you have been answering in class every day, on HW

o Also be ready for “what if” questions (small changes that require you to conjecture and explain more than perform additional calculations)

• Be sure to explain any assumptions you are making along the way

• Be prepared to think/explain/interpret

o Not just plug into formulas

o Be ready to explain process of how you would do calculations

§ e.g., p-value = P(X ≤ k), where X ~ Binomial(n, π)

o Be able to both make conclusions from a p-value (evaluate) and provide a detailed interpretation of what the p-value measures in context (interpret)

o Be succinct in your answers (using acceptable statistical terms helps with this, but don’t use them incorrectly)

• Read carefully

• Be sure to answer the question asked

• Take advantage of information provided

• Relate conclusions to context

• Prepare

o Re-work in-class investigations

o Re-work HW questions

o Work through examples

o Re-read wrap-up sections

o Come to Thursday’s class prepared with questions

o Bring questions to office hours, Canvas discussion boards

These are the most relevant formulas:

Normal approximation for : E() = , SD() =

Standardizing: (observation – mean)/std dev = (x-)/

One-sample z-test statistic:

One-sample (Wald) z-confidence interval: + z*

Plus Four 95% confidence interval: where

Sample mean: = Sample standard deviation: s =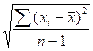

Binomial: P(X = k) = E(X) = n SD(X) =

Technology Summary (for reference)

· To calculate/estimate a probability from a binomial distribution knowing n and

o One Proportion Inference applet

o JMP: Distribution Calculator (Journal)

o R: iscambinomprob

· To calculate a probability from a normal distribution knowing mean and std dev

o Normal Probability Calculator Applet

§ Easy to label horizontal axis

o JMP: Distribution Calculator (Journal file)

o R: iscamnormprob

All three methods allow you to find the probability above, below, between, or outside values.

· To calculate a percentile from a normal distribution knowing mean and std (you know the probability and want to find the corresponding observation, z-score)

o Normal Probability Calculator Applet

§ Enter value in probability box and press enter or click mouse elsewhere

o JMP: Distribution Calculator (Input probability and calculate quantiles)

o R: iscaminvnorm

o FYI: With JMP and R, you can do something like this with the binomial distribution as well. You can also use trial and error, but explain the process

· To find critical values (z*) from a standard normal distribution (mean = 0, SD = 1)

o Normal Probability Calculator applet, specifying the tail probabilities (1-C)/2 and pressing Enter

o JMP: Distribution Calculator (Input probability and calculate quantiles)

o R: iscaminvorm

· To calculate the exact binomial p-value

o One proportion Inference applet

§ Check the Exact Binomial box

o JMP: Analyze > Distribution (one-sided alternative hypothesis)

§ Can also use Distribution Calculator

o R: iscambinomprob

· To approximate a binomial p-value

o Simulation: One Proportion Inference applet, especially when CLT does not apply

§ Make sure run enough repetitions for simulation-based p-value

§ Can also calculate exact binomial p-value, or normal approximation

o CLT: Theory-Based Inference Applet (one proportion)

§ Includes graph (can paste in raw data) and Ho/Ha statements

§ Uses normal approximation

§ Allows continuity correction

o JMP: (Journal) Hypothesis Test for One Proportion (z-test)

§ Includes Ho/Ha, p-value format

o R: iscamonepropztest

· To calculate an exact binomial confidence interval

o JMP: (Journal) Confidence Interval for One Proportion

o R: iscambinomtest

· To calculate a one-sample z-confidence interval

o Theory-Based Inference applet (one proportion)

o JMP: (Journal) Confidence Interval for One Proportion

§ If you use Analyze > Distribution you get the “score interval” (p. 79)

o R: iscamonepropztest

With 95% confidence, can use the Adjusted Wald by specifying two more successes and 4 more observations.

· To calculate power

o Power Simulation applet (simulation or exact or normal approximation)

§ Really just two copies of the One Proportion applet

o JMP: DOE > Sample Size and Power (binomial = Exact Clopper-Pearson)

o R: iscambinompower, iscamnormpower