Workshop Statistics: Discovery with Data, Second Edition

Topic 18: Central Limit Theorem

Activity 18-1: Smoking Rates

(a) q
(b) Not necessarily due to sampling variabilty.
(c) The CLT says that this sample proportion should have a normal distribution, with mean equal to q=.229, and standard deviation equal to sqrt(q(1-q)/n) = sqrt(.229*.771/100) = .042.
(d) Shade .25 and above. Guesses will vary from student to student.
(e) mean of sampling distribution: .229;  standard deviation of sampling distribution: .042;  z-score standardizing .25 = (.25-.229)/.042 = .5
(f) probability 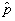above .5 = 1-.6915= .3085
(g) The sampling distribution based on a larger sample size will still be centered at .25, but will exhibit less variability: sqrt(.229(1-.229)/400)=.021. We expect these  values to fall closer to .229, so the probability of a sample result above .25 would be smaller.
(h) z=(.25-.229)/.021 = 1.00, proportion above = 1-.8413 = .1587
(i) Variabilty will decrease and a sample proportion above .25 will be even less likely.  z=(.25-.229)/sqrt(.229(1-.229)/1600) = 2, proportion above = 1-.9772= .0228
(j) no
(k) There would be no changes.
 

Activity 18-2: Smoking Rates (cont.)

(a) SD=sqrt(.142(1-.142)/100)=.035

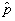    <-----------------  values ----------------->
(b) mean=.142, sd=.035
z=(.25-.142)/.035 = 3.09
proportion above = .001
So P(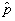>.25) = .001
(c) The standard deviation will decrease, which increases the z-score, which decreases the probability that the sample proportion would exceed .25.
(d) We would have strong reason to doubt that the state was Utah because there is such a small probability (.001) of there being any more than 25 smokers in a sample of 100 Utah residents that it would be hard to believe that a random sample of 100 Utah residents would yield 25 smokers.
 

Activity 18-3: Candy Bar Weights (cont.)

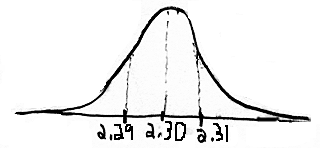
(a) Want P(2.18 < 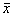< 2.22) where xbar follows a normal distribution with mean m=2.20 and standard devaition s=.04
Z(2.18) = (2.18-2.20)/.04 = -.5
proportion below -.5 = .3085
Z(2.22) = (2.22-2.20)/.04 = .5
proportion below .5 = .6915
Subtracting to find the area between = .6915-.3085 = .3830
(b) These sample means will have a normal distribution, centered at m=2.20, but now with standard deviation s/sqrt(5)=.04/sqrt(5) =.018

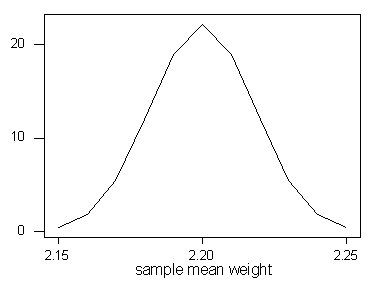
(c) shading
(d) The z-scores are (2.18-2.20)/.018 = -1.11 and (2.22-2.20)/.018 = 1.11, so the probability that the average weight of 5 candy bars will be between 2.18 and 2.22 ounces is .8665-.1335 = .7330.
(e) The probability will increase if the sample size were 40 instead of 5 because the standard deviation will decrease and the values will be more concentrated around 2.20, so there will be a greater concentration of sample mean values in this middle range between 2.18 and 2.22.
(f) The standard deviation of the sample means is now sigma/sqrt(n) = .04/sqrt(40) = .0063.  The z-scores are (2.18-2.20)/.0063 = -3.17 and (2.22-2.20)/.0063 = 3.17, so the probability that the average weight of 40 candy bars will be between 2.18 and 2.22 ounces is .9992-.0008 = .9984
(g) The calculations in (f) would remain approximately correct even if the candy bar weights themselves had a skewed, nonnormal distribution since the Central Limit Theorem establishes that the distribution of sample means will be approximately normal distribution for a sample size as large as n = 40.  The normal approximation would not be valid with n = 1 or n = 4.
 

Activity 18-4: Candy Bar Weights (cont.)

(a) SD(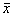)=.04/sqrt(60)=.00516
Z(2.19)=(2.19-2.20)/.00516 = -1.94, proportion below -1.94 = .0262
Z(2.21) =1.94, proportion below = .9738
probability of an 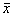 value beween 2.19 and 2.21 = .9476

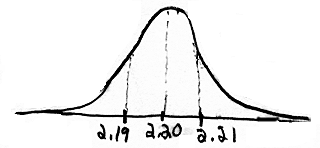
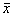     <-------------  values ------------------->
(b) The z-scores are the same as in (a), so the probability remains .9476.

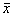     <-------------  values ------------------->
(c) They are equal.
(d) .9476, becuase the difference between the observation and the population mean is still  + .01, and the standard deviation does not change.
(e) There is a very high probability (.9476) that a sample of size 60 would result in a sample mean weight within + .01 of the actual population mean.
 

Activity 18-5: Solitaire (cont.)

(a) std dev(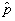) = sqrt(1/9(8/9)/10) = .099
z = (.10-1/9)/.099 = -.1122
proportion below = .4562
P(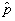<.10) = .4562
(b) .3079+.3849 = .6928 (Note: the probability of zero wins is .3079, not .0379 as appeared in some printings of the book.)
(c) These are not at all close.
(d) The CLT provides a poor approximation for each probability in this situation because the technical conditions concerning n and q needed for the validity of the CLT are not met.  n*q is only 1.11, which is not greater than or equal to 10.  n(1-q) is only 8.88, which is not greater than or equal to 10.