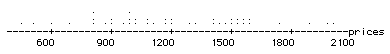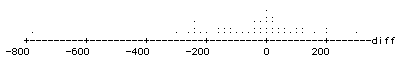Please write in the blue books provided. Show the details of your calculations. You may use a calculator, your book (including the table of standard normal probabilities and the t-table), your notes, and your homework solutions on this exam. . Notice that even though many questions contain multiple parts, you can answer later parts whether or not you correctly answer earlier parts. Also notice that some of the calculations are provided for you in many problems.

1. (20 points) A student wanted to assess whether her dog Muffin tends to chase one of her balls more often than the other. She rolled both a blue ball and a red ball at the same time and observed which ball Muffin chose to chase. Repeating this process a total of 96 times, the student found that Muffin chased the blue ball 57 times and the red ball 39 times.
a) In what proportion of the 96 tosses did Muffin chase the blue ball?
b) Is this number from a) a parameter or a statistic? Explain.
c) The student performed a significance test of 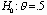 vs. 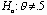, where  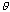represents the proportion of times that Muffin would chase the blue ball in the long run. Calculate the appropriate test statistic.
d) Determine the p-value of the test.
e) Would you reject the null hypothesis at the .01 significance level?
f) Report the smallest significance level 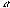 at which you would reject the null hypothesis.
g) Write a one-sentence conclusion to the student summarizing what the data reveal about whether her dog Muffin tends to chase one of her balls more often than the other.

2. (20 points) To investigate a possible relationship between heart disease and baldness, researchers asked a sample of 663 males suffering from heart disease to classify their degree of baldness on a five-point scale. They also asked a control group (not suffering from heart disease) of 772 males to do the same baldness assessment. The results are summarized in the table:
 

	none	little	some	much	extreme
heart disease	251	165	195	50	2
control	331	221	185	34	1

a) Identify the cases (observational units) in this study.
b) Is this a controlled experiment or an observational study? if it is an observational study, what kind is it? Explain briefly.
c) Calculate the proportion of heart disease patients who report some or more (i.e., some, much, or extreme) baldness. Also calculate the proportion of control group patients who report some or more baldness.
d) Perform the appropriate test of significance to determine if these sample proportions differ significantly at the .05 level. State the null and alternative hypotheses in symbols and in words, and report the test statistic and p-value. Include a one-sentence conclusion related to the context.
e) What conclusion do you draw regarding a possible relationship between baldness and heart disease?

3. (20 points) The following data are the prices of a sample of 41 prizes from the television game show The Price is Right:

 

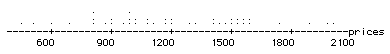
N	MEAN	MEDIAN	TRMEAN	STDEV	SEMEAN	MIN	MAX	Q1	Q3
41	1209.6	1169.0	1207.3	385.9	60.3	455.0	1995.0	929.5	1507.5

a) Let 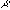 represent the mean price among all prizes awarded on this game show. Use the sample information to construct a 98% confidence interval for .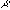
b) Without doing further calculations, indicate whether a test of significance addressing whether the sample data provide evidence that 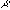 differs from $1000 would be significant at the .02 level. Explain your reasoning.
c) List the technical assumptions which underlie the use of this confidence interval procedure. Comment on whether the assumptions seem to be satisfied in this case.
d) What proportion of the 41 prizes have prices that fall within the interval? Should this proportion generally be close to .98? Explain briefly.
e) What proportion of the 41 prizes have prices that fall within two standard deviations of the sample mean?

4. (10 points) Suppose that a television news program conducts a call-in poll about a proposed city ban on handgun ownership, with the result that 1921 of 2372 calls oppose the ban. Suppose further that the news anchors make the following announcement: "81% of our sample opposed the ban, and we can be 95% confident that the true proportion of citizens who opposing a handgun ban is within 1.6% of the sample result."
a) Explain how the station calculated the 81% and 1.6% figures that it cites.
b) Is the station's conclusion justified? Explain.

5. (10 points) Researchers in England gathered data to study whether Friday the 13th has an effect on people's behavior. One part of their study involved comparing the numbers of shoppers at a sample of 45 different grocery stores on Friday the 6th and then on Friday the 13th. They then calculated the difference between the number of shoppers on the 6th and the number of shoppers on the 13th at each store. These differences (subtracting in the order 6th minus 13th) are displayed and summarized by Minitab below:

 

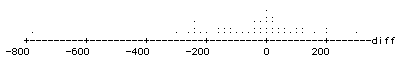
N	MEAN	MEDIAN	TRMEAN	STDEV	SEMEAN	MIN	MAX	Q1	Q3
45	-46.5	-11.0	-37.4	178.0	26.1	-774.0	302.0	-141.0	53.5

a) Write a few sentences describing the distribution of the sample of differences. Comment specifically on the researchers' conjecture that people alter their shopping habits on Friday the 13th as oppposed to Friday the 6th.
b) Perform the appropriate test of significance to assess whether the sample data support the researchers' conjecture. Report the null and alternative hypotheses, test statistic, and p-value. Also write a brief conclusion summarizing your findings.

6. (10 points) The May 3, 1998 issue of Parade magazine contains a discussion in the "Ask Marilyn" section about baseball games in which the winning team scores more runs in one inning than the losing team does in the entire game. Marilyn dubs such a game a "big bang" and claims that a "big bang" occurs in 50% of all games played. To investigate this claim, I examined the results of the 52 Major League baseball games played on May 1-4, 1998 and found that a "big bang" occurred in 18 of them.
a) One can use my sample data to calculate a 95% confidence interval to estimate the proportion of all Major League games in which a "big bang" occurs. The half-width of this interval turns out to be .139. Is this finding consistent with Marilyn's claim that a "big bang" occurs in 50% of all games? Explain briefly.
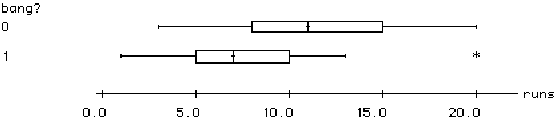
b) The following boxplots compare the distributions of total runs scored between games in which a "big bang" occurs (code=1) and games in which it does not occur (code=0). Write a sentence or two comparing these distributions. In particular, address the question of whether "big bang" games seem to occur more often in low scoring games or in high scoring games.

7. (5 points) Suppose that you take a random sample of 10,000 Americans and find that 1111 are left-handed. You perform a test of significance to assess whether the sample data provide evidence that more than 10% of all Americans are left-handed, and you calculate a test statistic of 3.70 and a p-value of .0001. Furthermore, you calculate a 99% confidence interval for the proportion of left-handers in the America to be (.103,.119). Consider the following statements:

8. (5 points) Students who study a foreign language in high school tend to perform better on the verbal portion of the SAT than do students who do not study a foreign language in high school. Can one reasonably conclude from this observation that studying the foreign language causes students to improve their verbal skills? Explain.