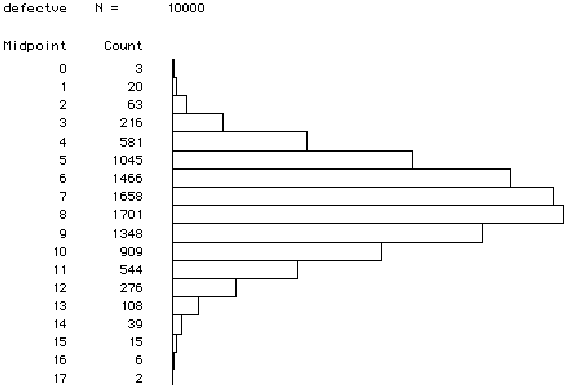
Please write in the blue books provided. Show the details of your calculations. You may use a calculator, your book (including the table of standard normal probabilities), and your homework solutions on this exam. Notice that even though many questions contain multiple parts, you can answer later parts whether or not you correctly answer earlier parts. Please note the point value on each problem and budget your time accordingly.

1. (5 points) In the Presidential election of 1968, Richard Nixon won 43.4% of the popular vote and Hubert Humphrey won 42.7% of the popular vote. In a Gallup poll conducted in September of 1967, 43% of those polled favored Nixon while 28% favored Humphrey. Identify which of these numbers are parameters and which are statistics.

2. (5 points) Suppose that two researchers Beth and Frank work together to study a simple random sample of subjects from a population, and they find that the sample proportion is equal to .8. When they construct a confidence interval based on this sample proportion, Beth comes up with (.73,.87) while Frank gets (.75,.89). Indicate which interval has to be wrong, and explain your choice.

3. (10 points) Suppose that an alien lands on earth, notices that there are two different sexes of the human species, and sets out to estimate the proportion of human beings who are female. Suppose that the alien chooses the members of the 1998 U.S. House of Representatives as its sample of human beings.
a) Use the information that 53 Representatives are female and 382 are male to produce a 95% confidence interval for the proportion of human beings who are female.
b) Does this interval provide a reasonable estimate of the proportion of human beings who are female? Explain.

4. (20 points) A student wanted to study the ages of couples applying for marriage licenses in Cumberland County, Pennsylvania. He studied a sample of 94 marriage licenses and found that in 67 cases the husband was older than the wife.
a) Use this sample information to construct a 92% confidence interval for the relevant population proportion.
b) Identify clearly the parameter of interest here.
c) Do the sample data provide evidence that the husband is usually older than the wife among couples applying for marriage licenses in Cumberland County, Pennsylvania? Explain briefly, based on your confidence interval.
d) If the student wanted to produce a 95% confidence interval with a margin-of-error of ±.04, how many couples would he need to sample?

5. (5 points) Suppose that SAT scores follow a normal distribution with mean 896 and standard deviation 174. Suppose further that Peter finds out that he scored in the top 3% of SAT scores. Determine how high Peter's score must have been.

6. (15 points) Suppose that the wrapper of a candy bar lists its weight as 8 ounces. The actual weights of individual candy bars naturally vary to some extent, however. Suppose that these actual weights vary according to a normal distribution with mean 8.5 ounces and standard deviation .325 ounces.
a) What proportion of the candy bars weigh less than the advertised 8 ounces?
b) If the manufacturer wants to decrease this proportion from a) by changing the mean of its candy bar weights, should it increase or decrease that mean? Explain briefly, without performing any calculations.
c) If the manufacturer wants to decrease this proportion from a) by changing the standard deviation of its candy bar weights, should it increase or decrease that standard deviation? Explain briefly, without performing any calculations.

7. (20 points) Suppose that 80% of all American college students send a card to their mother for Mother's Day. Suppose further that you plan to select a simple random sample of 250 American college students and to determine the proportion of them who send a card to their mother on Mother's Day.
a) Is 80% a parameter or a statistic? Explain. What symbol have we used to represent it?
b) According to the Central Limit Theorem, how would the sample proportion who send a card to their mother vary from sample to sample?
c) Determine the probability that between 75% and 85% of the sample send a card to their mother.
d) Without doing any calculations, indicate whether the answer to c) would be larger, smaller, or the same if 150 students had been sampled. Explain briefly.

8. (10 points) Suppose that a manufacturer has historically produced 30% defective items but that recent engineering modifications have been implemented in an effort to reduce the proportion of defectives. Suppose further that when a random sample of 25 items is inspected, 2 of the items are found to be defective. The following histogram displays the results of a simulation of 10,000 samples of 25 items each with a 30% defective rate.

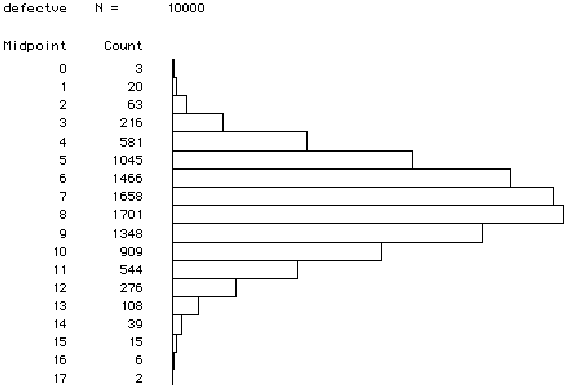
a) In how many of these 10,000 simulated samples were two or fewer of the items defective?
b) Based on this simulation result and on the sample finding that 2 of the 25 items sampled were defective, does the manufacturer have reason to believe that the engineering modifications have indeed reduced the defective rate? Explain.

9. (10 points) Your text says that "confidence intervals seek to estimate a population parameter with an interval of values calculated from an observed sample statistic." Demonstrate that you understand this statement by describing an example in which one could use a sample proportion to produce a confidence interval as an estimate of a population proportion. Clearly identify the population, sample, parameter, and statistic involved in your example. Do not use any example that appears in your book.