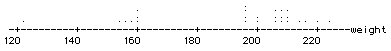
Please write in the blue books provided. When calculations are asked for, show the details of your work. When interpretations or explanations are called for, be clear and concise. You may use a calculator but may not use Minitab on any part of the exam. Please note the point value on each problem and budget your time accordingly; there are a total of ten problems.
1. (5 pts.) Identify the cases (observational units) in:
a) the "televisions and life expectancy" data that you analyzed in
class.
b) the "toy advertising" data that you analyzed for homework.
2. (15 pts.) The following dotplot displays the distribution of weights of the members of the 1996 U.S. Men's Olympic Rowing Team:
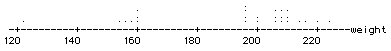
a) Estimate the value of the median of the distribution as accurately
as you can from this plot.
b) Would the mean would be greater than or less than the median for
these data? Explain briefly.
c) Write a paragraph describing key features of the distribution.
3. (5 pts.) Construct a hypothetical example of ten exam scores so that the inter-quartile range equals zero and the mean is less than the median.
4. (10 pts.) In addition to the two scoring methods for tennis that
you analyzed in a homework problem, a third scoring method called "handicap"
scoring was analyzed by a Dickinson College student researcher. He simulated
100 games played with this scoring method and recorded the length (measured
by number of points played) of each game. The results for these 100 games
are tallied in the table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) Determine the median of these
game lengths.
b) Determine the mode of these game
lengths.
c) Determine the range of these
game lengths.
5. (15 pts.) The following data are the weights in grams of 35 male house sparrows that survived a severe winter storm and of the 24 male sparrows that perished in the same storm:
survived:
23.2 23.6 23.7 23.8 23.9 24.1 24.2 24.3 24.3 24.5 24.6 24.7
24.7 24.8 24.9 25.4 25.6 25.7 25.7 25.7 25.7 25.9 26.2 26.2
26.3 26.3 26.5 26.6 26.7 26.7 26.9 26.9 27.0 27.9 28.0
perished:
24.6 24.6 24.9 25.0 25.0 25.1 25.5 25.6 25.6 25.8 25.9 26.0
26.0 26.0 26.0 26.1 26.5 26.5 27.1 27.5 27.6 28.3 28.3 31.1
a) Determine the five-number summary of the weights of the 35 sparrows that survived. (Note that these are already in order.)
The five-number summary of the weights
of sparrows that perished is:
|
|
|
|
|
|
|
|
|
|
|
|
b) Use this information to conduct
the outlier test for the weights of the sparrows that perished.
c) Comment briefly on whether the
data provide evidence that sparrows which survived the storm tended to
weigh more than those that perished.
6. (5 pts.) Suppose that scores on
this exam follow a symmetric, mound-shaped distribution with mean 75 and
standard deviation 8.
a) What can you say about the proportion
of students who score between 67 and 83 on the exam?
b) What can you say about the proportion
of students who score above 91 on the exam? Explain briefly.
7. (5 pts.) The midrange of a distribution of data is defined to be (minimum + maximum) / 2. The midhinge of a distribution of data is defined to be (lower quartile + upper quartile) / 2. Which of these is resistant to outliers? Explain briefly.
8. (20 pts.) The following table
lists the average temperature of a month and the amount of the electricity
bill for that month:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The regression line for predicting the bill from the temperature is: bill = 55.1 - 0.214 temp. A scatterplot of the data with the regression line drawn in follows:
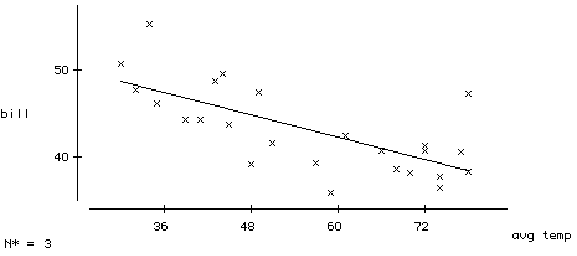
a) Use the regression line to predict
the electric bill for a month with an average temperature of 50 degrees.
b) Estimate as accurately as you
can form the scatterplot the proportion of variability in electric bills
that is explained by the regression line with average temperature.
c) Which month has the highest fitted
value? Explain your answer.
d) Without doing any calculations,
identify the month with the largest positive residual. Explain your answer.
9. (10 pts.) It is a demonstrable
fact that the sum of the residuals from a regression line must equal
zero.
a) Does it follow from this fact
that the mean of the residuals must equal zero? Explain briefly.
b) Does it follow from this fact
that the median of the residuals must equal zero? Explain briefly.
10. (10 pts.) Supose that a company
has just fired a total of 300 employees and that the gender breakdown is
as represented in the following table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
When the employees are further classified
according to whether their position is professional or clerical, the breakdowns
are as represented in the following tables:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) Consider just the clerical
employees for the moment. Calculate the proportion of clerical men who
were fired and the proportion of clerical women who were fired. Which is
higher?
b) It turns out in this case that
men have a higher proportion of being fired overall, but men have a lower
proportion of being fired among both professional and clerical employees.
Write a few sentences explaining why this reversal occurs, basing your
explanation on the data provided in the tables.