1) The following data are the point totals for the UOP Men's Basketball team in their first 8 victories this season:
80 72 68 55 80 78 90 85
(a) (5 pts) Make a stemplot of these winning point totals and describe
the shape of the distribution.
(b) (3 pts) Would the Five Number Summary or the mean and standard
deviation be a better summary for this distribution? Explain your choice.
2) Two investigators wanted to study the heights of 18-24 year old men
in Stockton. One investigator, Happy Harry, took a random sample of 100
men. The other investigator, Tired Tony, took a random sample of 1000 men.
(a) (2 pts) If each investigator finds the average height of the men
in his sample, which investigator, Harry or Tony, should find a larger
average, or will they be about the same? Explain.
(b) (3 pts) Which sample, Harry or Tony's, should have less bias or
will they be about the same? Explain.
(c) (3 pts) Which estimate of the population mean, Harry or Tony's,
should have higher precision, or will they be about the same? Explain.
3) In 1988, men averaged abut 500 on the math SAT, the standard deviation
was about 100, and their scores followed a Normal distribution. One of
the men who took the math SAT in 1988 will be picked at random, and you
have to guess his test score. You will be given 50 dollars if you guess
it right to within 50 points.
(a) (2 pts) What one number should you guess?
(b) (5 pts) With this guess, what is your probability of winning the
50 dollars?
Extra Credit: What is your expected winnings?
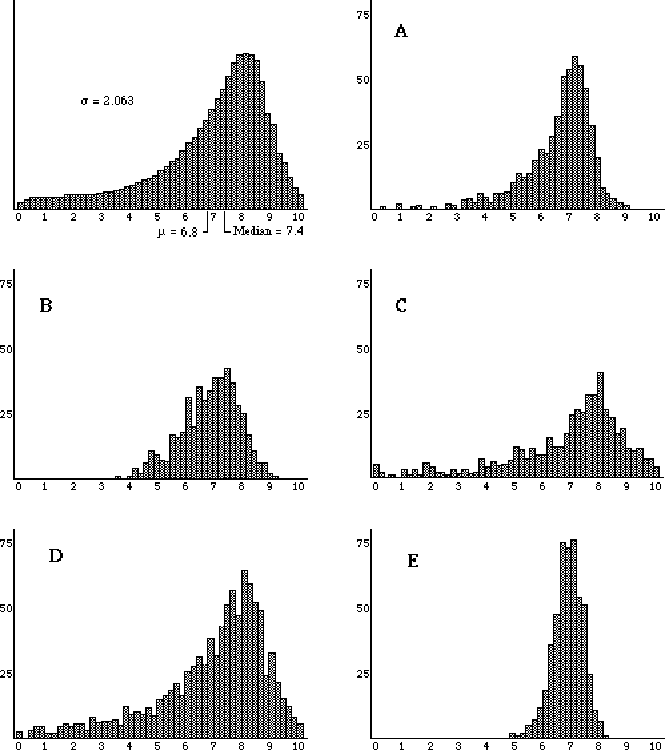
4) The distribution for a population of test scores is displayed below
on the left. Each of the other five graphs, labeled A to E represent possible
sampling distributions of sample means for 500 random samples drawn from
the population. (Justify choices)
(a) (2 pts) Which graph represents a sampling distribution of sample
means for samples of size 1? A B C D E
(b) (2 pts) Which graph represents a sampling distribution of sample
means for samples of size 9? A B C D E
Population Distribution

5) A social research scientist wants to test whether the percentage
of Republicans who favor the death penalty is greater than the percentage
of Democrats who are in favor of the death penalty. Suppose the sample
data showed that the percentage of Republicans who are in favor of the
death penalty is 42% and the percentage of Democrats who are in favor of
the death penalty is 40%.
(a) (2 pts) Write down the null and alternative hypotheses for this
test.
(b) (3 pts) The p-value for this test is .0021. The 95% confidence
interval for p1-p2 is (.00637,.03363). Which
of the following conclusions do you think is more appropriate to draw?
(c) (2 pts) Which conclusion does a p-value better support? Explain.
(d) (2 pts) Which conclusion does a confidence interval better support?
Explain.
6) In a clinical trial, data collection usually starts at "baseline",
when the subjects are recruited into the trial but before they are randomized
to treatment and control groups. Data collection continues until the end
of follow-up. Two clinical trials on prevention of heart attacks report
baseline data on weight, shown below.
| Number of persons | Average weight | Standard deviation | ||
| Trial 1 | Treatment | 1,012 | 185 lb | 25 lb |
| Control | 997 | 143 lb | 26 lb | |
| Trial 2 | Treatment | 995 | 166 lb | 27 lb |
| Control | 1,017 | 163 lb | 25 lb |
(a) (4 pts) In one of these trials, the randomization did not achieve
the desired result. Which trial and why do you say so? How will this affect
our results and conclusions for this study? (Hint: make sure you focus
on the most serious difficulty)
(b) (4 pts) Below are ten people and their weights. Randomly assign
them to one treatment group and a control group (start with line 139 of
Table B). Clearly show your work.
| Bob 148 | Tom 174 | Joe 148 | Fred 133 | Sam 157 |
| Curt 177 | Al 162 | Harry 188 | Gami 160 | Dan 188 |
7) Can pleasant aromas help a student learn better? Two researchers
believed that the presence of a floral scent could improve a person's learning
ability in certain situations. They had ten people work through a pencil
and paper maze 2 times, first wearing an unscented mask and then wearing
a scented mask. Tests measured the length of time it took subjects to complete
each of the two trials. They reported that, on average, subjects wearing
the floral-scented mask completed the maze more quickly than those wearing
the unscented mask.
(a) (3 pts) Is this an observational study, survey, or experiment?
Explain.
(b) (2 pts) Identify the response and explanatory variables.
(c) (4 pts) Explain how confounding makes the results of this study
worthless.
(d) (4 pts) Sketch an outline of a more appropriate design for the
study.
8) NCAA collected data on graduation rates of athletes in Division I
in the mid-1980s. Among 2,332 men, 1,343 had not graduated from college,
and among 959 women, 441 had not graduated.
(a) (3 pts) Set up a two-way table to examine the relationship between
gender and graduation.
(b) (3 pts) Calculate a couple of conditional percentages to
describe the relationship between gender and graduation.
(c) (3 pts) Identify a test procedure would be appropriate for analyzing
this relationship? State the null and alternative hypotheses.
(d) (3 pts) What type of distribution does the test statistic you describe
in (c) follow? For what values of this test statistic will you reject the
null hypothesis at the 5% level?
(e) (2 pts) If the above result is significant, would this mean that
if some people have a sex change they will increase their chance of graduating?
Explain briefly.
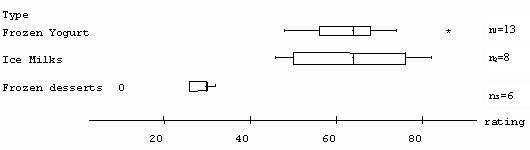
9) A panel of trained testers judged the flavor quality of different vanilla frozen desserts (frozen yogurts, ice milks, other frozen desserts) measured on a scale from 0 to 100. The data are from a Consumer Reports article "Low-fat frozen desserts: Better for you than ice cream?" (August, 1992). Below is a graphical summary of the data.
Here is most of the ANOVA output from the computer:
ANALYSIS OF VARIANCE ON rating
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
(a) (2 pts) Explain briefly why ANOVA was the appropriate analysis for
these data.
(b) (2 pts) State the null and alternative hypotheses.
(c) (4 pts) Finish the ANOVA table giving the F-statistic, degrees
of freedom, and approximating the p-value. Show your work. What is your
conclusion about the flavor quality of the different desserts?
(d) (2 pts) Based on the graph, do you feel the technical assumptions
needed for the validity of this test procedure are valid?
10) A random sample of 7 households was obtained, and information on
their income and food expenditures for the past month was collected. The
data (in hundreds of dollars) are given below.
| Income ($100's) | 22 | 32 | 16 | 37 | 12 | 27 | 17 |
| Food Expend ($100's) | 7 | 8 | 5 | 10 | 4 | 6 | 6 |
Here's the Minitab output:
The regression equation is
expend = 1.87 + 0.202 income
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s = 0.8181
R-sq = 85.9%
R-sq(adj) = 83.1%
Here's a scatterplot of these data with the regression line superimposed.
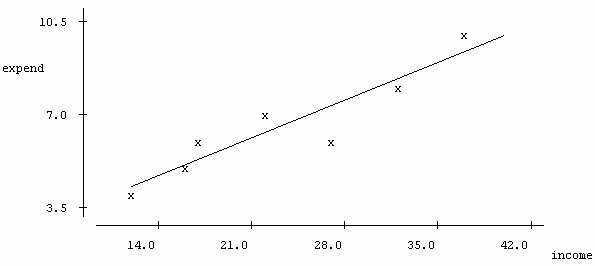
(a) (2 pts) Describe the direction and strength of the association.
(b) (2 pts) On the graph, identify the point which you think has the
largest residual. Explain.
(c) (2 pts) On the graph, identify the point which you think has the
most influence on the position of the regression line, and how the line
would change if it was removed. Explain.
(d) (3 pts) Provide an interpretation of the number .202 in the regression
equation in the context of these data. Exactly what does this value tell
us?
(e) (4 pts) Is there evidence of a statistically significant relationship
between income and food expenditure? Make sure you clearly explain the
basis for your answer.
(f) (2 pts) Explain why you would not recommend using this relationship
to predict the food expenditure for a household with an income of $5,200.
11) National data show that, on the average, college freshmen spend
7.5 hours a week going to parties. President DeRosa doesn't believe that
these figures apply at UOP. He takes a simple random sample of 50 freshmen,
and interviews them. He finds that the 95% confidence interval for the
number of hours spent a week going to parties is (5.72, 7.42).
(a) (4 pts) Explain to the President what he means by the phrase "95%
confidence".
Now he wants to test the hypothesis that the mean for UOP is different
from the national mean at a 5% significance level.
(b) (2 pts) Specify the null and alternative hypotheses for this test.
(c) (2 pts) Indicate a test procedure he could use to conduct this
test.
(d) (3 pts) Eager to gain favor with the president, you tell him that
you can save him lots of time because, based on the data already presented,
you know what he will conclude and he doesn't have to perform any additional
calculations. Does he reject or fail to reject the null hypothesis at the
5% level? Explain.
Extra Credit
Suppose you take 50 measurements on the speed of cars on Interstate 5, and that these measurements follow roughly a Normal distribution. Do you expect the standard deviation of these 50 measurements to be about 1 mph, 5 mph, 10 mph, or 20 mph? Explain.