![]() 1=
1=
![]() 2=
2=
![]() 3=
3=
s1=
s2=
s3=
Math 37 - Lecture 31
Analysis of Variance (Ch. 12)
Example Is the difference between average GPAs in the 7 schools at UOP significant?
How compare means? Can do 21 two-sample t tests. Problem:
Need to extend two-sample procedures into an overall test.
GOAL: Compare two or more population means.
NUMERICAL SUMMARIES: Sample means and standard deviations for each group.
GRAPHICAL SUMMARIES: Side by side boxplots or stemplots
Example Want to compare the average gas mileage of standard four-wheel drive pickup trucks manufactured by Chevrolet, Dodge, and Ford. An experiment is designed in which five vehicles of each type are randomly and independently selected from the population of four-shell drive trucks. Each vehicle is driven in a stationary position for the equivalent of 500 miles. The miles per gallon is computed.
Response variable= type=
Explantory variable= type=
|
Chevy |
15.2 |
15.4 |
14.8 |
14.4 |
14.7 |
|
Dodge |
14.8 |
14.4 |
14.3 |
14.1 |
14.4 |
|
Ford |
15.1 |
14.3 |
14.6 |
13.9 |
14.6 |
Notation Have I groups, ni observations in each group, i=1,...,I
xij is the jth observation in group i, N=total sample size
|
|
|
|
|
|
|
|
|
|
|
|
|
s1= |
|
|
s2= |
|
|
s3= |
INFERENCE Are the observed differences in the sample means enough to conclude that the population means are different, or are the observed differences what we might see by chance?
Hypotheses H0
Ha
(if we find a difference we don’t know exactly which means were different and would need to do follow-up analysis).
Compare variability in sample means to chance variation
test statistic = variability between the group means
variability within the groups
Variation within the samples
Assume the population variances are equal, pool the variances
![]()
=mean square for error (MSE)
Between sample variability=variability in sample means
overall mean = ![]() = (n1
= (n1![]() 1+n2
1+n2![]() 2+n3
2+n3![]() 3)/N
3)/N
MSG = Sni(![]() i-
i- ![]() )2/I-1 = mean square for groups
)2/I-1 = mean square for groups
Test Statistic =F0= MSG/MSE to compare the variabilities
Follows approximately an F distribution
If H0 is true, these are equal and F0 is about 1
If H0 is not true, MSG is bigger than expect by chance, F0 large
Use Table E to find the p-value, specifying 2 degrees of freedom
Numerator = I-1 Denominator=N-I
Minitab Commands
MTB > oneway c1=c2
(observations in c1, subscripts in c2)ANALYSIS OF VARIANCE ON mpg
|
SOURCE |
DF |
SS |
MS |
F |
p |
|
car |
2 |
0.700 |
0.350 |
2.50 |
0.124 |
|
ERROR |
12 |
1.680 |
0.140 |
|
|
|
TOTAL |
14 |
2.380 |
|
|
|
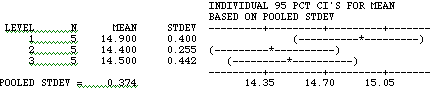
Technical Assumptions
- Populations are independent (check data collection description)
- Populations are Normal (check nscores of residuals)
- All of the populations have the same variance (check for ratio of largest standard deviation to smallest standard deviation<2)
Interaction - Does the effect of one explanatory variable on the response depend on the value of a second explanatory variable?