Math 37 - Lecture 13
Sampling Distributions
Statistics Parameters Type
![]() "sample mean" m ="population mean"
"sample mean" m ="population mean"
![]() "sample proportion" p="population proportion"
"sample proportion" p="population proportion"
Example Consider the population of Reese's Pieces candies manufactured by Hershey. Suppose that you want to learn about the distribution of colors of these candies but that you can only afford to take a sample of 25 candies. Take a random sample of 25 candies and record the number and proportion of each color in your sample.
|
orange |
yellow |
brown |
||
|
number |
||||
|
proportion |
1) Is the proportion of orange candies among the 25 that you selected a parameter or a statistic?
2) Is the proportion of orange candies manufactured by Hershey’s process a parameter or a statistic? What symbol represents it?
3) Do you know the value of the proportion of orange candies manufactured by Hershey?
4) Do you know the value of the proportion of orange candies among the 25 that you selected?
5) Did every student in the class obtain the same proportion of orange candies?
Sampling Variability: How does the value of the statistic behave in repeated random samples?
- Construct dotplot of the sample proportions of orange candies obtained by the students in the class = Sampling Distribution
0 .04 .08 .12 .16 .20 .24 .28 .32 .36 .40 .44 .48 .52 .56 .60 .64 .68 .72 .76 .80 .84 .88 .92 .96 1.00
- If every student was to estimate the population proportion of orange candies by the proportion of orange candies in his/her sample, would everyone arrive at the same estimate?
- Would they be close?
- Guess the population proportion of orange candies (random apts)
- How would the dotplot have looked different if each student had taken a sample of 75 candies instead of 25? Pool your results with 2 neighbors and add this combined ![]() to a new dotplot. How do they compare?
to a new dotplot. How do they compare?
0 .04 .08 .12 .16 .20 .24 .28 .32 .36 .40 .44 .48 .52 .56 .60 .64 .68 .72 .76 .80 .84 .88 .92 .96 1.00
Example: On the handout are the members of the U.S. senate. Consider this your population.
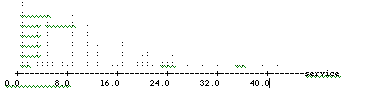
|
N |
MEAN |
MEDIAN |
TRMEAN |
STDEV |
SEMEAN |
|
|
Service |
100 |
11.52 |
9.00 |
10.70 |
9.60 |
.960 |
Shape?
Is 11.52 years a parameter or a statistic?
Use your random number table to select a simple random sample of 10 senators. Record the years of service for these 10 senators:
Find the mean years of service for the 10 senators in your sample:
Is the mean years of service in your sample a parameter or a statistic?
Does the mean years of service in your sample equal that of the population?
+---------+---------+---------+---------+---------+-------average service
0.0 7.0 14.0 21.0 28.0 35.0
Where is the center of the means from the students in class?
What is the sample of this distribution?
How often did we observe a mean exceeding 15 years?
Below is a sample of 30 senators and their years of service,

Is the variability of your 30 values less than the variability of your 10 values?
Describe the shape:
Sampling Distribution of ![]() with n=30 senators in each sample:
with n=30 senators in each sample:

- Is the variability of the sample means based on 10 values less than the variability of the sample means based on 30 values?
- Describe the shape:
Key Observations: Sampling Distributions (all possible samples)
|
Sample Mean, |
Sample proportion, |
|
|
Centered near |
Population mean m |
Population proportion p |
|
Standard deviation |
SD( |
SD( |
|
Shape |
Approximately normal for large n |
Approximately normal if n is large |
Members of the U.S. Senate (1998)
|
ID |
Name |
Yrs |
ID |
Name |
Yrs |
|
1 |
Abraham |
3 |
51 |
Hutchinson |
1 |
|
2 |
Akaka |
8 |
52 |
Hutchison |
5 |
|
3 |
Allard |
1 |
53 |
Inhofe |
4 |
|
4 |
Ashcroft |
3 |
54 |
Inouye |
35 |
|
5 |
Baucus |
20 |
55 |
Jeffords |
9 |
|
6 |
Bennett |
5 |
56 |
Johnson |
1 |
|
7 |
Biden |
25 |
57 |
Kempthorne |
5 |
|
8 |
Bingaman |
15 |
58 |
Kennedy |
36 |
|
9 |
Bond |
11 |
59 |
Kerrey |
9 |
|
10 |
Boxer |
5 |
60 |
Kerry |
13 |
|
11 |
Breaux |
11 |
61 |
Kohl |
9 |
|
12 |
Brownback |
2 |
62 |
Kyl |
3 |
|
13 |
Bryan |
9 |
63 |
Landrieu |
1 |
|
14 |
Bumpers |
23 |
64 |
Lautenberg |
16 |
|
15 |
Burns |
9 |
65 |
Leahy |
23 |
|
16 |
Byrd |
39 |
66 |
Levin |
19 |
|
17 |
Campbell |
5 |
67 |
Lieberman |
9 |
|
18 |
Chafee |
22 |
68 |
Lott |
9 |
|
19 |
Cleland |
1 |
69 |
Lugar |
21 |
|
20 |
Coats |
9 |
70 |
Mack |
9 |
|
21 |
Cochran |
20 |
71 |
McCain |
11 |
|
22 |
Collins |
1 |
72 |
McConnell |
13 |
|
23 |
Conrad |
11 |
73 |
Mikulski |
11 |
|
24 |
Coverdell |
5 |
74 |
Moseley-Braun |
5 |
|
25 |
Craig |
7 |
75 |
Moynihan |
21 |
|
26 |
D'Amato |
17 |
76 |
Murkowski |
17 |
|
27 |
Daschlee |
11 |
77 |
Murray |
5 |
|
28 |
DeWine |
3 |
78 |
Nickles |
17 |
|
29 |
Dodd |
17 |
79 |
Reed |
1 |
|
30 |
Domenici |
25 |
80 |
Reid |
11 |
|
31 |
Dorgan |
6 |
81 |
Robb |
9 |
|
32 |
Durbin |
1 |
82 |
Roberts |
1 |
|
33 |
Enzi |
1 |
83 |
Rockefeller |
13 |
|
34 |
Faircloth |
5 |
84 |
Roth |
27 |
|
35 |
Feingold |
5 |
85 |
Santorum |
3 |
|
36 |
Feinstein |
6 |
86 |
Sarbanes |
21 |
|
37 |
Ford |
24 |
87 |
Sessions |
1 |
|
38 |
Frist |
3 |
88 |
Shelby |
11 |
|
39 |
Glenn |
24 |
89 |
Smith, Bob |
7 |
|
40 |
Gorton |
9 |
90 |
Smith, Gordon |
1 |
|
41 |
Graham |
11 |
91 |
Snowe |
3 |
|
42 |
Gramm |
13 |
92 |
Specter |
17 |
|
43 |
Grams |
3 |
93 |
Stevens |
30 |
|
44 |
Grassley |
17 |
94 |
Thomas |
3 |
|
45 |
Gregg |
5 |
95 |
Thompson |
4 |
|
46 |
Hagel |
1 |
96 |
Thurmond |
42 |
|
47 |
Harkin |
13 |
97 |
Torricelli |
1 |
|
48 |
Hatch |
21 |
98 |
Warner |
19 |
|
49 |
Helms |
25 |
99 |
Wellstone |
20 |
|
50 |
Hollings |
32 |
00 |
Wyden |
2 |