Math 37 - Lecture 10

Normal Distribution cont.

How do we decide if our data is normally distributed?

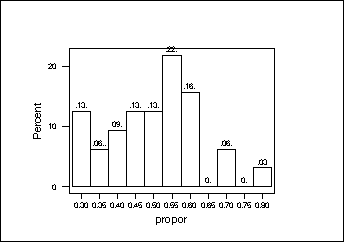
Our Distribution:

=.4984, s=.1247

Ideal Normal Distribution:

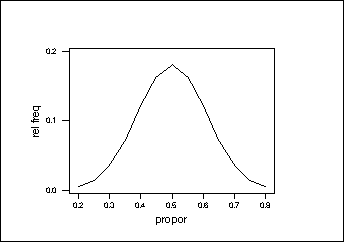
m=.5, s=.11

1) Graph the data

Look for outliers, skewness, gaps, clusters

2) Check the 68-95-99.7 Rule

Calculate the intervals

See if your data has roughly the right percentage in each.

Use and s if don't have idealized values

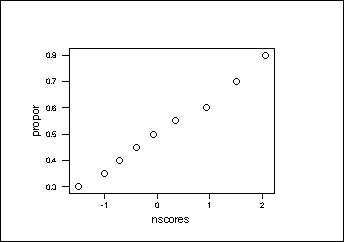
3) Normal Probability Plots (aka Normal Quantile Plots)

Compare your n data points to the n points you would expect to see from a Nromal distribuiton. The plot sees if your numbers are similar. If so, the plot will be a straight line.

MINITAB: MTB> nscores c1 into c2

MTB> plot c1 c2

Common Shapes:

Example 1 For the following data, find the mean and standard deviation

24 27 31 31 33 36 39 40 43 44 45 45 49 50 63

What percentage of the observations are below 44.5?

Subtract the mean from each observation, and divide each observation by the standard deviation (can round a bit).

Distribution of standard scores has mean and variance

Standard Normal Distribution

What percentage of these new observations are below .45?

What the relationship between 44.5 for the original data and .45 for the new data?

How do the percentages compare?

How does this relate to standard scores and percentiles?

Example 2 Last semester, the distribution of Prof. Passer's final grades had a mean of 74 and a standard deviation of 7, and Prof. Nauphel's had mean 78 and standard deviation 18. Both give A's if the final score is above 90.

- Which professor gives a higher proportion of A's?

- Which professor gives a higher proportion of F's (below 60)?

Example 3 Calculating Percentage Between

Sketch the Standard Normal curve(mean 0 and standard deviation 1).

Shade the region below z=-2, and find the percentage below z=-2.00. Now shade the region below 3 and find the percentage below.

What part of your curve is double shaded?

Look at the shaded region above z=-2 and below z=3. How would you find the percentage in that interval? Suggest a general rule.

The level of cholesterol in 14 year old boys has approximately a Normal distribution with mean 170 mg/dl and standard deviation 30 mg/dl. What proportion of 14 year old boys have a cholesterol level between 160 and 240 mg/dl?

Example 4 Calculating an Observation given a Percentile.

Remember Professors Passer and Nauphel? Well another professor on campus has said he will only give A's to the top 10% of scores on the final exam, regardless of actual scores. If the distribution of scores on the final turns out to be Normal with mean 69 and standard deviation 9, how high does your score have to be to earn an A? Suggest the formula for finding the value of X if you are given the percentile.