Stat 217 Review 1 Problem Solutions

 

1) a. Blood type - categorical

b. Waiting time – quantitative (if recorded as number of minutes between arrival and seen by doctor).

c. Mode of arrival (ambulance, personal car, on foot, other) - categorical

d. Whether or not men have to wait longer than women – this is a research question/comparison, not a variable posed to individual visitors (the variables asked of the visitors would be length of wait and gender)

e. Number of patients who arrive before noon – this is a summary of the data, not a variable posed to individual visitors, the variable would be whether or not the patient arrived before noon

f. Whether or not the patient is insured - categorical

g. Number of stitches required – quantitative

h. Whether or not stitches are required - categorical

i. Which patients require stitches – a subgroup of the sample, not a variable posed to individual visitors (see g and h)

j. Number of patients who are insured – this is a summary of the data, not a variable posed to individual visitors (see f)

k. Assigned room number – categorical (numerical but doesn’t make sense to talk about “average” room number)

 

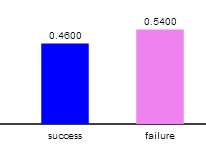
2) a. A bar graph showing the proportion that landed up (success) and the proportion that landed down (failure):

b. The parameter of interest is the underlying long-run probability of a spun racquet landing up.

c. Null hypothesis: the probability of landing up is .50 ( = .5)

Alternative hypothesis: the probability of landing up is not .50 (  .5)

We are using a two-sided alternative hypothesis because we wouldn’t want to use this method to see who serves first if either the racquet lands up more than half the time or if it lands up less than half the time. 

 

d. Flip a coin 100 times and record the time of times the coin lands heads.  Let this represent the racquet landing “up.”  Repeat this process a large number of times and look at the distribution of the number of heads across all these trials.  Then see where 46 falls in this distribution.  If it falls is in the tail of the distribution, we have evidence that the racquet was not landing equally heads/tails in the long-run.  If 46 falls among the “typical” values in this distribution, then we don’t have evidence against the belief that the racquet is 50/50 when spun this way.

 

e. The graph that is centered at 0.50, our hypothesized probability of success is the correct one (the one on the left).

f. From this output, we see that 0.46 is not unusual for a 50/50 coin. Therefore, we would not consider a result of 46 “ups” and 54 “downs” to be surprising if the racquet spinning truly was a 50/50 process.  We do not have convincing evidence that this is not a 50/50 process.

 

To calculate a p-value here, we would consider results “or more extreme” to be those further away from 50 in either direction. We would see how often we got 46 or fewer heads OR 54 or more heads (aka 46 or fewer tails).  Adding these together would give us our p-value.

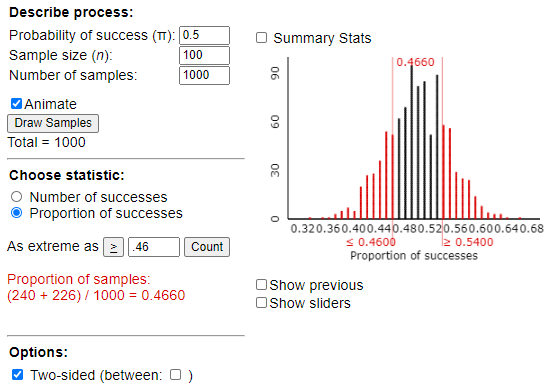
Two-sided simulation-based p-value = 0.4660 This is not a small p-value (e.g, .466 > .05), so we fail to reject the null hypothesis.

 

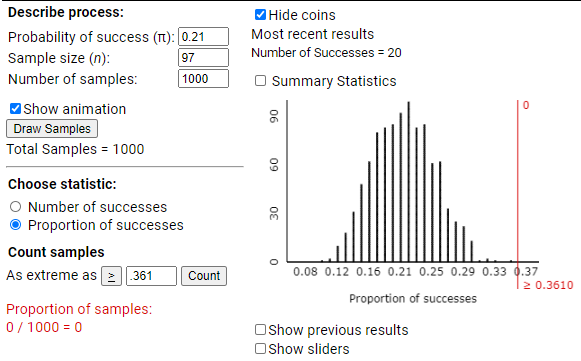
3) a. The population is all Cal Poly students and the sample is the 97 who responded.

b. The parameter is the proportion of all Cal Poly students who eat breakfast 6 or 7 times a week. We could call this (unknown) value . The statistic is the proportion of the sampled students who report eating breakfast 6 or 7 times a week. We know the second number to be  = 35/97 = .361.

Note: .21 is the population proportion at James Madison, not  or .

 

To find the p-value, we can consider two approaches, simulation and theory-based.

For the simulation approach we can use the One Proportion applet (note we are assuming the population here is much larger than the sample, more than 20 times larger). We want to set the sample size to be 97 and we are going to conduct the simulation assuming the proportion of all Cal Poly students is also .21 as it was at James Madison University. Then we see how often random samples from such a population yield a sample proportion of .361 or higher (the direction conjectured by the researchers).

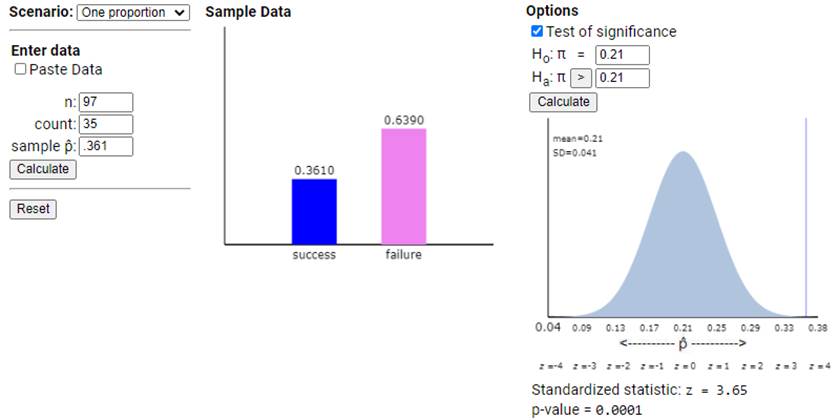
Alternatively, we could consider using the normal approximation because there were 35 “successes” and 62 “failures,” both at least 10, so the approximation should be valid. Using the Theory-Based Inference applet

 

 

We again find a very small p-value. In addition, this applet tells us that our observed statistic (observed = .361) is 3.65 standard deviations above the hypothesized value for  of .21.

 

 

c. The p-value is clearly small (.001 < .05), so we reject the null hypothesis that , the proportion of all Cal Poly students who eat breakfast 6 or 7 times as week, equals .21, in favor of the alternative the hypothesis that  > .21.  Thus, we conclude that there is convincing evidence that more than 21% of all Cal Poly students eat breakfast 6 or 7 times a week. So at least on this measure of “healthiness” we have strong evidence that the Cal Poly population is healthier.

 

d. The p-value says that if we were to repeatedly take simple random samples of 97 students from a population with  = .21, then in less than .1% (depending what you find for the p-value) of those samples would we find our sample proportion  who eat breakfast at least 6 times a week to be .361 or higher.

 

e. The statistic () will probably be different but not the parameter ().  The population parameter is a fixed (but unknown to us) value.

 

f. This indicates a potential source of sampling bias. Those who chose to respond to the survey could be different from those who did not.  Perhaps they are more aware of their eating habits and more interested in health overall and that’s why they were more likely to reply, leading to an overestimate of the population proportion in this study.

 

g. We need a list of all Cal Poly students (the sampling frame) probably from the registrar’s office.  Assign everyone on the list a unique 5 digit number.  Then use a random number table or computer or calculator to randomly select 1590 unique ID numbers.  Find and survey those students.

 

h. If there is still a high nonresponse rate, even with the larger sample size we would still be concerned about how representative the sample is.  It would be much, much better to recontact the originally selected people (several times if necessary) to get their responses than to simply sample more people.

 

i. With the larger sample size and the same value for the statistic we would expect the p-value to be even smaller.  The sampling distribution of the sample proportions (’s) would cluster even closer around .21 (less sampling variability) and it would be even more shocking to randomly obtain a sample proportion as extreme as .361 when  = .21.

 

4) a. The sample size was 100 and had 46 up and 54 down, both above 10. So yes, we would predict a normal shape to the distribution of sample proportions.

b. We are 95% confidence that the probability a spun racquet lands heads is between .3656 and .5575.  That is, if we spin the racquet forever, then in the long run we expect between 36.6% and 55.8% to land up.

c. The confidence interval should get narrower (less wide) with the larger sample size.

d. Well, we can’t say this for sure, but we can say .5 is a plausible value for the probability of landing up because .5 is captured inside our 95% confidence interval. In other words, it’s plausible that if we repeatedly spun this racquet forever, it’s plausible the racquet would land up 50% of the time in the long run.

 

5) The simulation p-value is more accurate, because the theory-based computation requires at least 10 successes and failures. In this case, there are only 4 students who study at least 35 hours per week---not enough for an accurate theory-based (large sample) p-value.

 

 

6)

a.    In this context  represents the average IQ of all people who claim to have had an intense experience with an UFO.

b.    This is a one-sided test, because we wish to test whether or not the average IQ of this group is greater than 100.

c.    In order for this procedure to be valid, either a normally distributed population (not a bad assumption for IQ scores) or a large sample size (25 > 20 but not by much).  We also want the population (everyone who has seen a UFO) to be more than 20 x 25 = 500 (may not know this?)

d.   

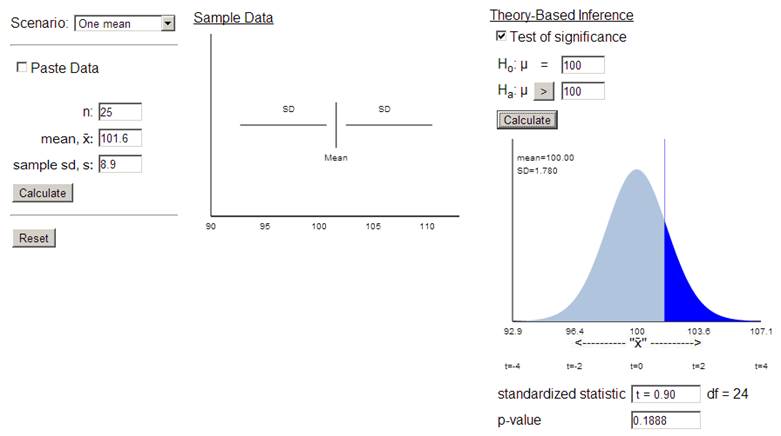
    = 0.90  

e.    From the graph, we can ballpark the p-value between .1 and .33 (actual value .19).  Based on the t value being less than 1 and the large amount shaded on the graph, this sample mean of 101.6 is not a surprising outcome for a random sample of 25 people when the population mean equals 100.

f.    If the average IQ of this group is really 100, then we could expect to see a random sample of 25 people from this group with an average IQ of at least 101.6 in about 19% of samples by random chance alone.  As this would be a fairly common occurrence, we have no reason to doubt that the mean IQ of the population (those who claim to have had an intense experience with an UFO) is 100. We also need to be willing to believe that this sample is representative of all individuals who claim to have had such an experience.

 

 

7) a. The observational units are the adult American who were interviewed by the GSS.  The variable is the number of close friends that the adult American has.  This variable is quantitative.

b.         A t­-interval is valid in spite of the strong right skew because the sample size is very large (1467).

c.    95% confidence interval for , the mean number of number friends in the population of all adult Americans: 1.987 +  2(1.7708/√1467)

= 1.987 +  .0924

= (1.894, 2.079)

Note: Theory-based approach gives (1.896, 2.078)

We are 95% confident that the mean number of close friends in the population of American adults is between 1.894 and 2.079 friends.

Note, if we calculate 1.987 +  2(1.7708), we extend from below zero to about 4.4 friends.  Meaning about 95% of adult Americans report between 0 and 4.4 friends.  This is very different from the confidence interval which is a statement about the population mean, not individual adults.

d.    The reasonable interpretations of this interval are:

e.    “Ninety-five percent of all people in this sample reported a number of close friends within this interval” is incorrect because that is not what 95% confidence refers to (the percentage of intervals that will capture μ, not the percentage of the sample that does something)

       “If you took another sample of 1467 people, there is a 95% chance that its sample mean would fall within this interval” is incorrect because we are not trying to capture sample means – we are trying to capture the population mean.           

       “If you repeatedly took random samples of 1467 people, this interval would contain 95% of your sample means in the long run” is not a correct interpretation because the interval would definitely contain the one sample mean you used to create the interval.  We cannot predict how many of the other sample means it would contain – the interval procedure is estimating the population mean.  We are not saying other sample means should be within 2 standard deviations of the one we observed, but that sample means in general should fall within 2 standard deviations of the actual population mean.

       It is incorrect to say “this interval captures the number of close friends for 95% of the people in the population” because this interval estimates the mean number of friends – not the number of individual friends for any person.

f.     If the sample size were large, the interval would have the same midpoint, but would be narrower.

       If the sample mean were larger the interval would have a larger midpoint, but would have the same width.

       If the sample values were less spread out, the standard deviation would be smaller, so the margin-of-error would be smaller, so interval would be narrower (but would have the same midpoint).

If every person in the sample reported one more close friend, the sample mean would be larger (by 1), so the midpoint of the interval would increase by 1, but the width would be unchanged.           

 

8) (a) The population is all American households. The sample is the 47,000 (ish) households for which they received a response about whether or not they included a pet cat.

(b) This tells us that the observed sample proportion (0.324) is 4.14 standard deviations below the hypothesized population proportion (one-third).

(c) Yes, the standardized statistic is large (4.14 > 2) and the p-value is small (< 0.0001), so we have strong evidence to reject the null hypothesis in favor of the alternative hypothesis.  This was presented as a two-sided test (the not equals to in Ha), so we conclude there is evidence that the population proportion of households that include a bit cat differs from one-third. 

(d) To answer this question, about the size of the difference, I would look at the confidence interval rather than the test of significance. The confidence interval (0.3198, 0.3282) is consistent with the test in that 1/3 is not included among the plausible values. However, they are not all that far from 1/3, telling us the percentage is around 32% more than 33%, but that if we wanted to tell folks that the percentage is roughly 33%, we wouldn’t be considered huge liars.

 

This example highlights the distinction between statistical significance (could this have happened by chance alone) and practice significance (is it all that meaningful to you or me). Often we might need to consult a “subject matter expert” to decide is the size of a difference is meaningful, that’s not usually the statistician’s call.