Extension

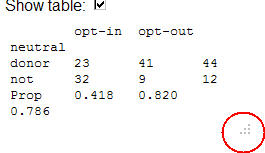
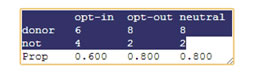
Suppose we had obtained the following table:

 
Opt in
Opt out
Neutral
Total

Donor
4
8
8
20

Non-donor
6
2
2
10

Total
10
10
10
30

(t) Verify that the conditional proportions are similar as those for the actual research study. Do you think these results will provide more, less, or the same strength of evidence against the null hypothesis? Explain.

 

(u) Are the technical conditions for the validity of the Chi-squared distribution as a mathematical model for our null distribution met for these data? Clearly explain how you are deciding.

 

(v) Let's verify this:

  • Enter this new two-way table into the applet:
    • In the Show table display box, carefully change the 6 cell entries to these 6 numbers (e.g., 23 to 4, 41 to 8, etc.).
    • (Note: You can pull down on the right corner of the display box to enlarge it so the columns don't wrap around.)
    • Use your mouse to select the first three rows (the treatment group labels, the donor and not now rows, including the row labels)- don't take the conditional proportions.

table

two-way table
  • Use ctrl-C to copy this information, press Clear under the Sample data entry box, click inside the box, and then ctrl-V to paste.
  • Then press the Use Table button.
  • The applet should convert this information to the two variables and the "Show table" output should stay the same.
  • Now create 1000 shuffles of the Chi-squared statistic and check the box (if not already) to show the X2 output. Enter the observed value of the Chi-squared statistic for this new table into the Count Samples box and press Enter.
  • Make a screen capture of this null distribution and the X2 output and paste into your report .

 

Does the Chi-squared distribution appear to be a reasonable model for this null distribution? Do you obtain a similar p-value using the simulation method and using the theoretical (Chi-squarde distribution) method? (Cite your results.)

 

Back Next