Example 1: Wording of Questions

Example 1: Wording of Questions

Researchers have conjectured that the use of the words “forbid” and “allow” can affect people’s responses to survey questions. Students in an introductory statistics class were randomly assigned to answer one of the following questions:

· Should your college allow speeches on campus that might incite violence?

· Should your college forbid speeches on campus that might incite violence?

Of the 11 students who received the first question, 8 responded yes. Of the 14 students who received the second question, 12 said no.

(a) Identify the observational units and the explanatory and response variables.

(b) Is this an observational study or an experiment? If an observational study, suggest a potential confounding variable. If an experiment, explain the roles of randomization and blinding in this study.

(d) Construct a segmented bar graph to display these results and comment on the relationship revealed by this graph.

(e) Based on earlier studies, researchers expected people to be less likely to agree to “forbid” the speeches, leading to more no responses (and thus appearing to be in favor of having the speeches), while they expected people to be comparatively less likely to agree to “allow” the speeches. Do these data provide strong evidence that these students responded more positively toward having such speeches if their question was phrased in terms of “forbid” rather than “allow”? Carry out Fisher’s Exact Test, being sure to define your random variable and explaining the decision you would make based on the p-value. Write a paragraph summarizing your conclusions including whether a cause-and-effect conclusion can be drawn and the population you are willing to generalize these results to.

(f) In a 1976 study, one group of subjects was asked, “Do you think the United States should forbid public speeches in favor of communism?”, while another group was asked, “Do you think the United States should allow public speeches in favor of communism?”. Of the 409 subjects randomly asked the “forbid” version, 161 favored the forbidding of communist speeches. Of the 432 subjects asked the “allow” version, 189 favored allowing the speeches. Construct a segmented bar graph for these data and comment on whether you believe the p-value for this table will be larger or smaller than that in (e). Explain your reasoning.

Analysis:

(a) The observational units in this study are the statistics students. The explanatory variable is the word choice in the question they responded to (categorical) and the response variable is whether their response was in favor of the speeches (yes with the allow question and no with the forbid question, categorical).

(b) This was an experiment since the questions were randomly assigned to the students. Presumably the instructor mixed up the order of the questionnaires prior to passing them out to the students. This is important to equalize other variables between these two groups such as political inclinations and gender. The students did not know that there were two different forms of the questions, so they study was blind. If they had realized that the instructor was focusing on how they responded to the two words, they probably would have responded differently eliminating any subconscious effect of the word choice.

	allow	forbid	total
Success	8	12	20
Failures	3	2	5
Total	11	14	25

(d) Segmented bar graph, with word choice along the horizontal axis, and success defined as favoring the speeches (yes to the allow question and no to the forbid question).

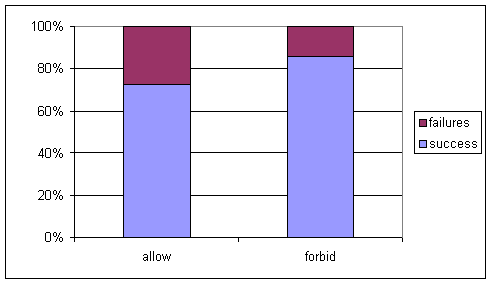
We see that most of these students were in favor of the speeches (80%). There was a slight tendency for those responding to the forbid question to appear more in favor (more likely to say no, do not forbid the speeches), .877 versus .727. However, the distribution within the bars look fairly similar and the association does not appear to be strong.

(e) If we assume there is no effect due to the wording of the question, Fisher’s Exact Test indicates how often we expect to see as few as 8 or fewer successes in the allow group (equivalently, at least as many as 12 successes in the forbid group). So if we define X to be the number in the allow group in favor of the speeches, the p-value will be P(X<8).

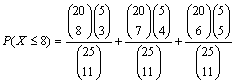= .3783

Confirming our calculations using Minitab:

Hypergeometric with N = 25, M = 20, and n = 11

x P( X <= x )

8 0.378261

Thus, if the word choice in the question had no effect, we would get experimental results a least this extreme about 38% of the time. This indicates that our experimental data is not surprising and does not provide evidence that the wording of the question had an effect on these students. Thus, we will not say the word choice in the question made a difference (though if the p-value had been small, since this was a randomized experiment, a cause-and-effect conclusion would have been valid). Furthermore, we should be hesitant in generalizing these results beyond introductory statistics students at this school. We do not know how these students were selected from this school nor whether these students might be representative of other college students. Perhaps this is a private school or the students tend to be more liberal than at other schools.

(f) If we again look at a segmented bar graph:

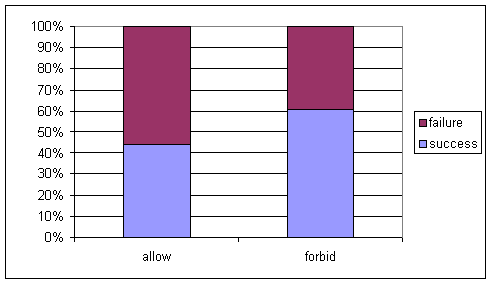
We see that in this study, individuals were less likely to be in favor of the speeches in general (52%). More importantly, the difference between the two groups is a bit larger (.606-.438=.169 in thus study, compared to a difference of .130 before), providing stronger evidence that such a difference would not happen due to chance alone and thus a smaller p-value. We must also take into account the fact that the group sizes are much, much larger in this study. With such large sample sizes, even small differences between the groups may appear statistically significant. Thus, with the larger samples and the slightly larger difference in success proportions, the p-value from this study will be much smaller than that from the original study.