Stat 414 – Review 1 Problems

The following are previous exam problems and application problems. The exam this quarter will also involve some more “conceptual” problems as you have been seeing on the quizzes. I also expect interpretation of output I provide. You won’t be using R live on the exam but I could ask you questions about R commands. You should assume all of the questions below have “Explain” after them.

1) Knee injuries, like tears in the ACL (a ligament in the knee) can lead to trabecular bone loss and post-traumatic osteoarthritis, but can bone health improve over time? The output below relates to a study on mice where one knee of each of 36 mice had the ACL (a ligament in the knee) ruptured and then measurements were taken of the bone area mass in the knee for both the healthy knees and the injured knees over 56 days after the injury.

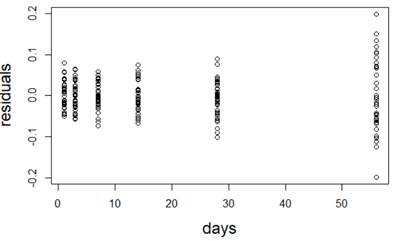
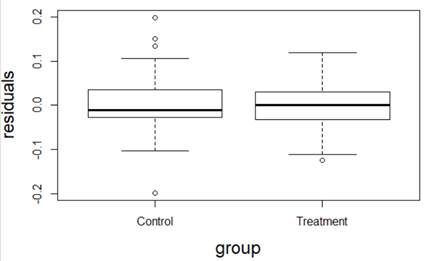
(a) I have fit a rather complicated single-level nonlinear model to these data (using days and group as explanatory variables). Assess the validity of my model. Be very clear how you are evaluating each assumption:

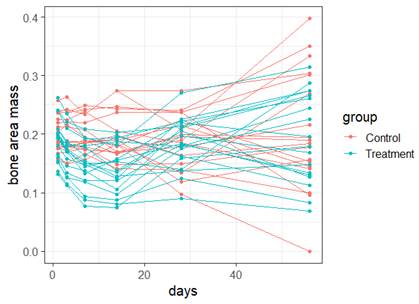
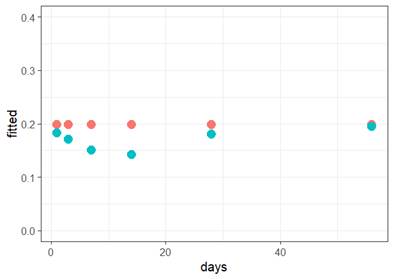
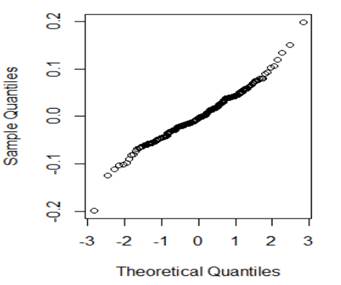
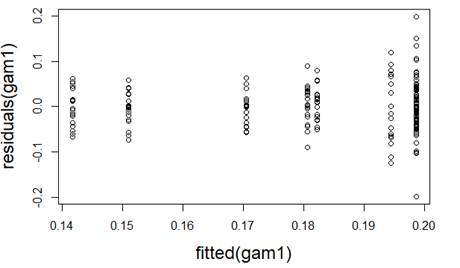
(b) Which of the following would you consider doing next to improve the validity of the model? Briefly justify your choice(s).

· Transformation to improve linearity

· Quadratic model to improve linearity

· Transformation of response to improve normality

· Transformation of explanatory to improve normality

· Include days in a weighted regression

· Include group in a weighted regression

· Multilevel model using mouse as a grouping variable (Level 2 units)

2) Here is another model for the FEV data

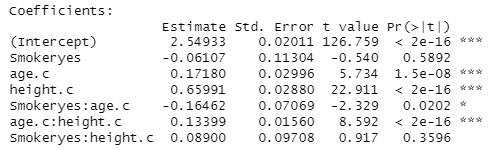
(a) Interpret the interaction between age and height in this context.

(b) How do you decide whether the interaction between age and height is statistically significant?

(c) How do you decide whether the association between age and height is statistically significant?

(d) Smoker doesn't appear to be very significant in the above model. Can I just remove it from the model?

(e) State the null and alternative hypotheses for removing Smoker from the model. Is the p-value for this test in the above output?

(f) What do you learn from the output below?

3) Recall our Squid data

Squid$fMONTH = factor(Squid$MONTH)
plot(Testisweight ~ fMONTH, data=Squid)

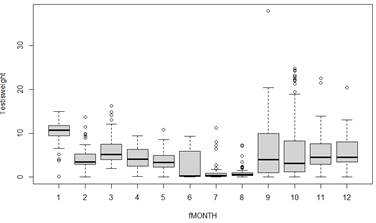
(a) Why did we create fMONTH?

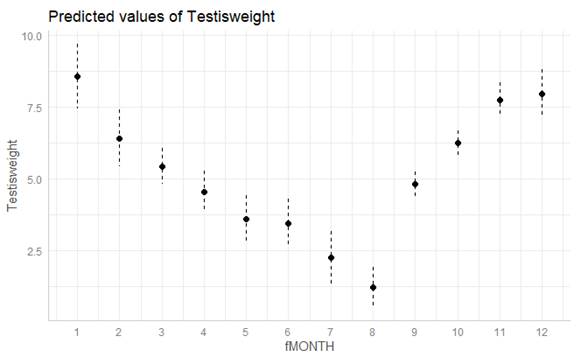
(b) Is there seasonality in the data? Does the variability in the response appear to vary by month? Identify 3 months where you think our predictions of Testisweight will be most accurate. Least?

The graph below shows the predicted values for each month (along with standard errors).

(c) If this model was fit with indicator coding and fMONTH = 1 as the reference group, is the coefficient of fMONTH2 positive or negative?

(d) If this model was fit with effect coding, is the coefficient of fMONTH2 positive or negative?

(e) Continuing (d): If fMONTH1 is the missing category, will its coefficient be positive or negative?

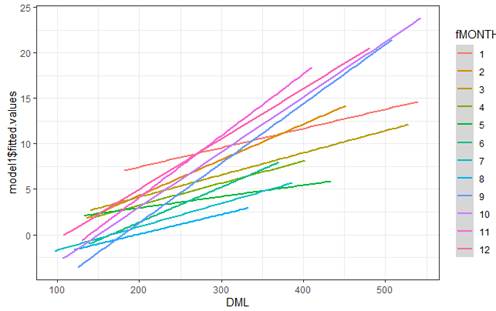
These are the fitted lines for the model that includes the interaction between fMONTH and DML

(f) How many terms does including this interaction add to the model?

(g) Will the coefficient of fMONTH10*DML be positive or negative?

But for addressing the unequal variance: We don't want to assume a "linear relationship" between the variability in the residuals and month number, so we will estimate the variance for each month. We can do that by finding the sample variance for each month.

(h) Which months do we want to 'downweight' in estimating the model?

(i) Conjecture what changes you would expect to see in the previous two graphs in this weighted regression model.

(j) How do you expect the residual standard error to change?

4) Trinh and Ameri (2018) collected data on 1,561 Airbnb listings in Chicago from August 2016, and then they merged in information from the neighborhood (out of 43 neighborhoods in Chicago) where the listing was located. Some of the variables included

· price = price for one night (in dollars)

· overall_satisfaction = rating on a 0-5 scale

· room_type = Entire home/apt, Private room, or Shared room

· neighborhood = neighborhood where unit is located (1 of 43)

(a) Identify the Level 1 units and the Level 2 units

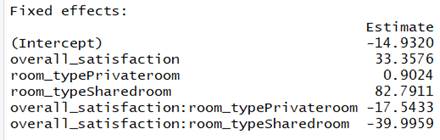
Consider the following output (Indicator parameterization was used for room size)

Fixed effects:
 Estimate Std. Error t value
(Intercept) 25.353 26.454 0.958
overall_satisfaction 24.919 5.508 4.524
room_typePrivateroom -82.739 3.831 -21.598
room_typeSharedroom -105.875 10.960 -9.660

> anova(model1)
Analysis of Variance Table
 Df Sum Sq Mean Sq F value
overall_satisfaction 1 41558 41558 8.0542

room_type 2 2593431 1296715 251.3102

(b) Is the type of room statistically significant? State the null and alternative hypothesis in terms of regression parameters, and clearly justify your answer.

(c) Suppose the model with the interaction was as shown below. Describe the nature of the interaction in this context.

5) Consider the following two models for predicting language scores for 9 different schools. IQ_verb is the student’s performance on a test of verbal IQ.

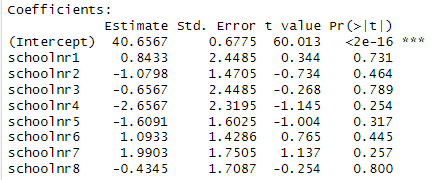
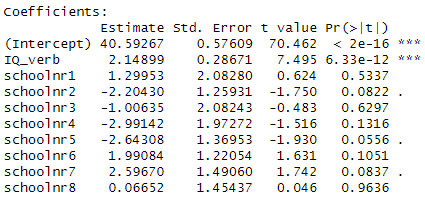
Which model demonstrates more school-to-school variability in language scores?