Stat 414 – HW 7

Due midnight, Friday, Dec. 1

You don’t need to include R code I give you but should include R code you create/modify and relevant output.

1) Toenail dermatophyte onychomycosis (TDO) is a common toenail infection where the nail plate becomes separated from the nail bed. Traditionally, antifungal compounds have been used to treat TDO. New compounds have been developed in an attempt to reduce the treatment duration. The data in toenail.txt are from a randomized, double-blind, multi-center study comparing two oral treatments ((Itraconazole and Terbinafine) over a 3-month period, with measurements taken at baseline, every month during treatment, and ever 3 months afterwards, with a maximum of 7 measurements per subject. At each visit, the target nail is coded as 0 (not severe, none or mild separation) or 1 (moderate or severe = complete separation). The research questions are whether the probability of severe infection decreases over time, and whether that evolution differs between the two treatments.

#library(readr)
toenail = read.table("https://www.rossmanchance.com/stat414/data/toenail.txt", header=TRUE)

toenail$ttmt = factor(toenail$ttmt)

(a) Explain what is measured by the time variable in this dataset.

(b) Explore the data:

with(toenail, round(tapply(y, list(ttmt, time), mean), 2))

#there is something wrong with interaction.plot, so let’s use this instead

props = ave(toenail$y, by = list(toenail$time, toenail$ttmt))

ggplot(data = toenail, aes(y=props, x=time, group=ttmt, col = ttmt)) +

geom_line() +

theme_bw()

Include the output and briefly summarize what you learn. (Be clear what the y-axis represents in the graph.)

(c) First fit a model that treats the observations on each individual as independent:

model1 = glm(y ~ time*ttmt, family = binomial, data = toenail)

summary(model1)

Is the interaction close to significant? How would you interpret the interaction in this context?

(d) Descriptively, how does the behavior of the fitted model compare to that of the raw data?

 ggplot(data = toenail, aes(y = fitted.values(model1), x = time, color = ttmt)) +
   geom_line(aes(group=ttmt)) + 
 labs(title = "glm", xlab="time", ylab="estimated prop") +
   theme_bw() + ylim(0, .5)

plot(effects::allEffects(model1))

(e) Now fit the multilevel model

model2 = glmer(y ~ time*ttmt + (1 | SubjID), family = binomial, data = toenail, nAGQ = 50)

#adaptive Gause-Hermite Quadrature, nAGQ = 50

summary(model2, corr=F)

#Include one of the following graphs!

plot(effects::allEffects(model2))

fits = predict(model2,re.form=NA,newdata=toenail) #fixed effects only

fits=exp(fits)/(1+exp(fits) #convert log odds to predicted probabilities

 ggplot(data = toenail, aes(y = fits, x = time, color = ttmt)) +
   geom_line(aes(group=ttmt)) + 
 labs(title = "mlm", xlab="time", ylab="estimated prop") +
   theme_bw() + ylim(0, .5)

plot(ggeffects::ggpredict(model2, terms=c("time", "SubjID [sample=9]"), type="re"), ci = F)

Does this model suggest a significant difference in the rate of decline between the two treatments? Explain how you are deciding.

You may have noticed that these models look pretty different. That’s because they estimate different things! Previously, we interpreted the slope coefficient of a fixed effect in a multilevel model as the “effect” of changing x-variables within a specific group or “on average,” the marginal effect in the population. With logistic regression models, the “within individual” rate of decline is not the same as the “overall average” rate of decline (partly because of the nonlinear back transformation). The slope of the marginal relationship applies to a randomly selected person (population average). The slope of the conditional relationship applies to a particular individual. The difference between these values increases as the cluster curves are more spread out (larger variance of the intercepts).

One approach is the convert the conditional (“subject specific”) slope to the marginal (think population average) coefficient, with the equation:

(f) For the above model, what is the marginal slope for time? Which is larger here, the subject-specific slope or the population-average (group level) slope? Does that make sense in context? Explain.

Alternatively, we can use generalized estimating equations (GEEs) to come up with parameter estimates and robust standard errors (think ‘sandwich estimators’). First, fit a model with a “bad correlation structure.”

install.packages("gee")

model3 = gee::gee(y ~ time*ttmt, family = binomial, data = toenail, id = SubjID,

corstr = "exchangeable", scale.fix = TRUE, scale.value = 1)

summary(model3)

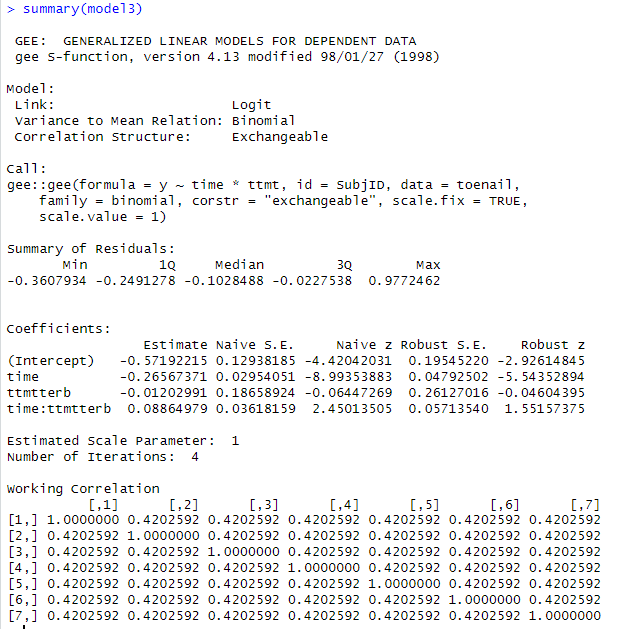
(g) Why do I consider the “working correlation matrix” assumptions to be unreasonable in this context?

Now allow for a more appropriate correlation matrix:

model4 = gee::gee(y ~ time*ttmt, family = binomial, data = toenail, id = SubjID,

corstr = "unstructured")

summary(model4)

 ggplot(data = toenail, aes(y = fitted.values(model4), x = time, color = ttmt)) +
   geom_line(aes(group=ttmt)) + 
 labs(title = "gee", xlab="time", ylab="estimated prop") +
   theme_bw() + ylim(0, .5)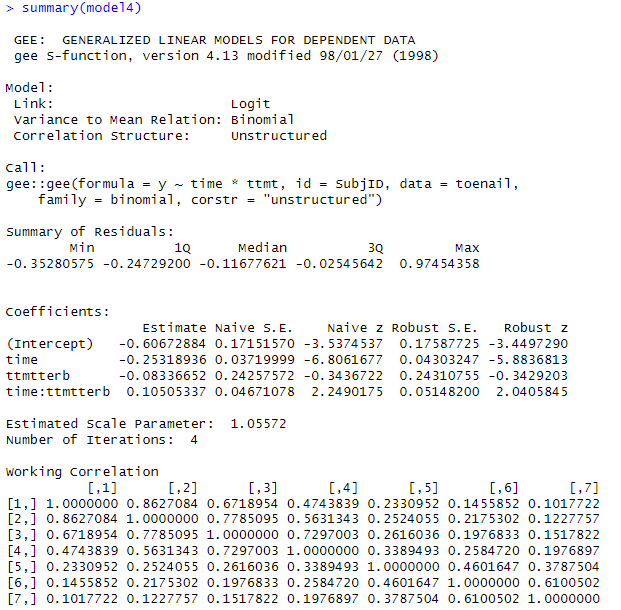

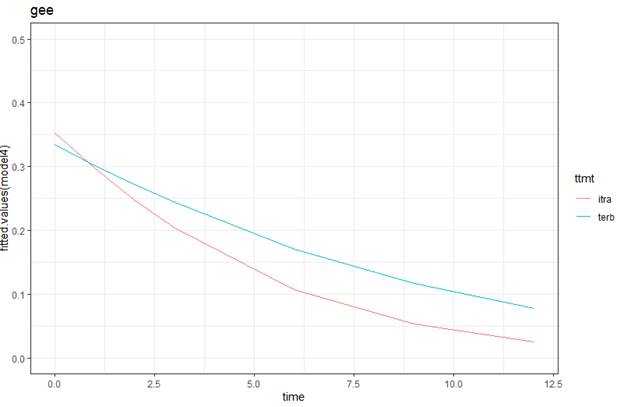
(h) What do you notice about the pattern of correlations in the “working correlation matrix”? Is the correlation modelled as the same between any two observations on the same individual? Does that make sense in this context?

(i) For models 3 and 4, how do the “robust standard errors” (which ‘correct’ for the dependence in the data) compare to the “naïve standard errors”? Is this what we expect to see? Explain. For which model are they more different?

(j) Which are closer to the observed proportions of severe infections, the marginal (population-averaged) values or the conditional (subject-specific) values?

head(fitted.values(model2), 10)
head(fitted.values(model4), 10)

Decent reference on GEEs vs. MLMs

(k) Suggest a good candidate for a “level 3” in this study.

2) In this exercise you will analyze data from the Scotland Neighborhood Study (Garner and Raudenbush, 1991). This study set out to test the hypothesis that a neighborhood's level of social deprivation has a negative effect on a student’s educational attainment even after controlling for the student’s prior attainment and family background. The data consist of 2,310 students who attended 17 secondary schools and resided in 524 neighborhoods (for one “school district”). Scottish secondary schools teach students from age 11-12 to the end of compulsory schooling (age 15-16). The response variable is a total attainment score (approximately standardized), based on a series of national examinations (the GSCE) taken at the end of compulsory secondary schooling in Scotland (age 16). Successful performance in these examinations is a crucial factor in decisions regarding employment or further post compulsory education possibly leading to entrance to universities. Higher scores indicate higher attainment. Predictor variables include student level verbal reasoning and prior reading attainment scores on entering secondary education, a range of family level background characteristics, and a neighborhood-level deprivation score.

install.packages("haven") #to be able to open a STATA data file

library(haven)

GCSE <- read_dta("https://www.rossmanchance.com/stat414/data/GCSE.dta")

head(GCSE)

(a) Are these data purely hierarchical? (e.g., are neighborhoods nested within schools?)

head(with(GCSE, table(neighid, schid)), 20)

(b) Summarize what you learn from the following commands (you may want to run parts of the commands/do further exploration of the data to see what is going on, please document)

(library tidyverse)

schoolcombos<- GCSE %>% select(schid,neighid) %>% unique()
summary(tapply(schoolcombos$neighid, as.factor(schoolcombos$schid), length))
summary(tapply(schoolcombos$schid, as.factor(schoolcombos$neighid), length))
 
Hints: Maybe also consider

table(GCSE[GCSE$schid == 0,]$neighid)

table(GCSE[GCSE$neighid == 29,]$schid)

(c) Fit the null (unconditional) model with separate school random effects and neighborhood random effects. (Model 0)

model0 = lmer(attain ~ 1 + (1|schid) + (1|neighid), data = GCSE, REML = FALSE)

summary(model0)

Briefly interpret the 3 variance estimates.

(d) Is the model with random effects a significant improvement over the single-level model without random effects?

modelNR = gls(attain ~ 1 , data = GCSE, method = "ML")

summary(modelNR)

logLik(model0)

logLik(modelNR)

(e) Summarize what you learn from the following output

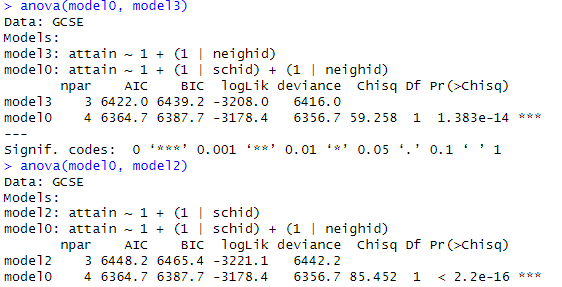
(f) Back to your null model in (c). What percentage of variation is explained by each component (i.e., variance partition coefficients or VPCs)? Are the “educational disparities” larger among schools or among neighborhoods?

(g) To calculate the correlation between two students (ICCs), you need to consider which components they share.

- Two students in the same school and neighborhood =

- Two students in the same school but different neighborhoods: =

What is the formula for two students in the same neighborhood but different schools?

Calculate the three ICC values. Which of these correlations is largest? Does this make sense in context? Explain briefly.

(h) Examine the normality of each of the random effects, e.g.,

qqnorm(ranef(model0)$schid[[1]])
qqnorm(ranef(model0)$neighid[[1]])

What do you conclude/suggest next?

(i) So far, we have assumed “additive effects” for the schools and neighborhoods. Let’s consider a model that allows for an interaction between the schools and neighborhoods.

 Try something like: combos = paste(as.character(GCSE$schid), as.character(GCSE$neighid))

model1 = lmer(attain ~ 1 + (1|schid) + (1|neighid) + (1 | combos), data = GCSE, REML = FALSE)

summary(model1)

anova(model0, model1)

How many terms does this add to the model? Is this model a significant improvement over the additive model? (Include relevant output and be clear how you are deciding.) Does the random interaction variance appear substantial? (Include relevant output and be clear how you are deciding.) Provide a brief interpretation of the implications of this interaction in context.

(j) Now add two measures of prior attainment: verbal reasoning (p7vrq) and reading scores (p7read). Are these variables jointly significant? (Include relevant output and be clear how you are deciding.) How much school-level variance and how much neighborhood-level variance and how much Level 1 variance is explained by these two variables? What does it tell you if these variables explain any Level 2 variance?

(k) Suggest a potential school-level variable that could be included (not necessarily one in the current data set). Suggest a potential neighborhood-level variable that could be included (not necessarily in the current data set).

3) The U.S. National Longitudinal Study of Youth (NLSY) original study began in 1979 with a nationally-representative sample of nearly 13,000 young people aged 14 to 21. CurranData.txt contains data from a sub-study of children of the female NLSY respondents which began in 1986 when the children were aged between 6 and 8 years. Child assessments (e.g., reading scores) were then measured biennially in 1988, 1990 and 1992. The sub-sample of 221 children were assessed on all four occasions.

(a) Read in two datasets. The first is in “wide format” and the second is in “long format.” What is the difference in these formats?

CurranDataWide <- read.delim("https://www.rossmanchance.com/stat414/data/CurranData.txt", "\t", header=TRUE)

head(CurranDataWide)

CurranDataLong <- read.delim("https://www.rossmanchance.com/stat414/data/CurranData_Long.txt", "\t", header=TRUE)

head(CurranDataLong)

(b) Look at the first few rows in wide format. Which are time-varying variables and which are time-invariant?

(c) Summarize what you learn from the “spaghetti plot” (pick one to include)

library(tidyverse)

ggplot(data = CurranDataLong, aes(y = RAscore, x = Time)) +

geom_line(aes(group=id), color="light grey") +

geom_smooth(aes(group=1), color="black", size=1) +

theme_bw() +

labs(x="Years since 1986", y="Reading Score")

OR

ggplot(CurranDataLong, aes(x = Time, y = RAscore, group = id)) +

geom_smooth(method = "loess", alpha = .5, se = FALSE) +

geom_smooth(aes(group=1), color="black") +

theme_bw()

(c) Examine the correlations of the reading scores across the four time points. (Explain what the R code is doing.) How would you summarize their behavior? Explain why the pattern in the covariation/ correlation makes sense in this context.

cor(select(CurranDataWide, contains("reading")))

(d) If we were to fit an OLS model to these data, what assumption would this model make about the correlations of the four observations on each person? Does that assumption seem reasonable here?

(e) Use lme (not lmer) to fit a random intercepts longitudinal model (meaning, include Time). Tell me about the variable Time. Report the intra-class correlation coefficient. What assumptions does this model make about the correlations of the four observations on each person? Does that assumption seem reasonable here?

library(nlme)

summary(model1 <- lme(RAscore ~ Time, random = ~1 | id, data = CurranDataLong))

cov2cor(getVarCov(model1, type="marginal")[[1]])

(f) Fit a random slopes model and examine the covariance matrix. Verify the values for var(y₁₁) = variance of “first observation” for person 1, var(y₂₁) = variance of “second observation” for person 1 (which can differ because we are using random slopes), cor(1,2) = correlation of the first two measurements on each person, cor(1,3) = correlation of first and 3rd measurement on each person. (Show me the numbers!) How are the variances changing over time? How do the correlations change as the observations get further apart?

model2 = lme(RAscore ~ Time, random = ~Time|id, data = CurranDataLong)

summary(model2)

getVarCov(model2, type="marginal")

cov2cor(getVarCov(model2, type="marginal")[[1]])

fits = fitted.values(model2)

ggplot(data = CurranDataLong, aes(y = fits, x = Time)) +

geom_line(aes(group=id)) +

theme_bw()

(g) Return to the basic two-level random intercepts model with time and time² as Level 1 variables, but without random slopes. Fit the AR(1) error structure. Is this model significantly better than the “independent errors” random intercepts model?

model4 = lme(fixed = RAscore ~ Time + I(Time*Time), random = ~1| id, correlation = corAR1(), data = CurranDataLong)

summary(model4); intervals(model4)

cov2cor(getVarCov(model4, type="marginal")[[1]])

model5 = lme(fixed = RAscore ~ Time + I(Time*Time), random = ~1| id, data = CurranDataLong)

anova(model5, model4)

(h) What is the estimated parameter of the AR(1) model (“autocorrelation”). How do you interpret it? Does there appear to be correlation between adjacent observations even after conditioning on student?

(i) How would we decide whether the pattern of growth (i.e., reading progress) differs between males and females? Explain the process, you don’t have to carry out.