Stat 301 – Review 2
Problems Solutions
1) Weights of 30 (fun-size) Mounds candy bars and 20 (fun-size) PayDay candy bars, in grams, are
shown in the dotplots below.
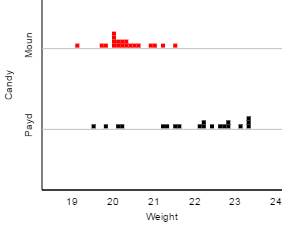
(a) Which
distribution would you consider skewed to the right?
The
Mounds distribution is a bit skewed to the right and the PayDay distribution is
strongly skewed to the left.
(b) Which
distribution do you expect has a larger mean?
The
PayDay distribution is clearly centered around larger values than the Mounds
distribution.
(c) Which
distribution do you expect has a larger standard deviation?
The
PayDay values are more spread out/less consistent than the Mounds distribution.
In
other words, the Mounds weights are more consistent, but occasionally a few weigh more. The
PayDay distribution is less predictable and often has weights that are much
lower than typical, perhaps the difference of one or two peanuts?
(d) Which
distribution would you suspect will have its mean larger than its median?
Mounds
because it is skewed to the right
2) The highway miles per gallon rating of the 1999 Volkswagen
Passat was 31 mpg (Consumer Reports, 1999). The fuel efficiency that a
driver obtains on an individual tank of gasoline naturally varies from tankful
to tankful. Suppose the mpg calculations per tank of gas have a mean of ![]() = 31 mpg and a standard deviation of
= 31 mpg and a standard deviation of ![]() = 3 mpg.
= 3 mpg.
(a) Would it be
surprising to obtain 30.4 mpg on one tank of gas? Explain.
Not
really, 30.4 is well within one standard deviation of the “population” mean of
31.
z =
(30.4 – 31)/3 = -0.20
(b) Would it be surprising for a sample of 30
tanks of gas to produce a sample mean of 30.4 mpg or less? Explain, referring
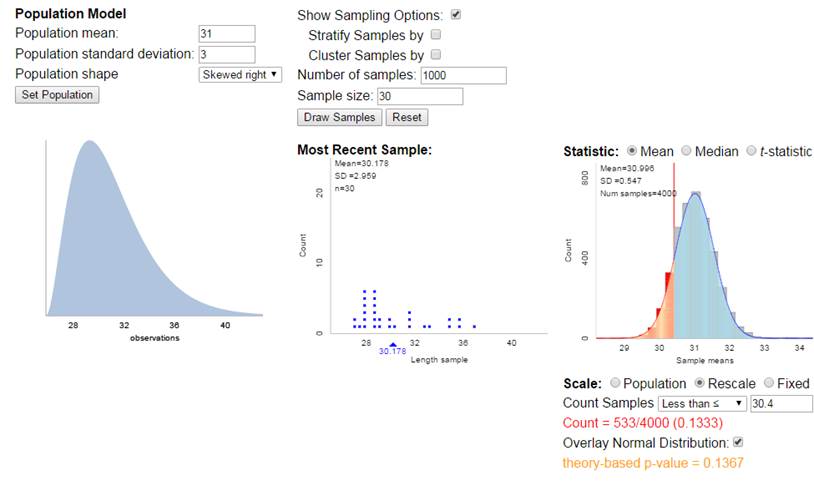
to the CLT and to a sketch that you draw of the sampling distribution.
First,
does the CLT apply here? We don’t know
much about the shape of the population distribution, though it’s reasonable to
assume the mileage from different tanks will by symmetric and roughly normal. But we also don’t care too much because our
sample size of 30 is considered large.
We are also assuming these observations are taken under identical
conditions.
So we
will model the distribution of the averages of 30 tanks for be normally
distributed with mean equal to 31 mpg and standard deviation equal to 3/sqrt(30) = 0.5477 mpg.
So a sample mean of 30.4 mpg would be (30.4 – 31)/.5477 = -1.095
standard deviations below the mean. This
is still not larger than 2.
Using
the normal distribution, P(![]() < 30.4)
< 30.4)
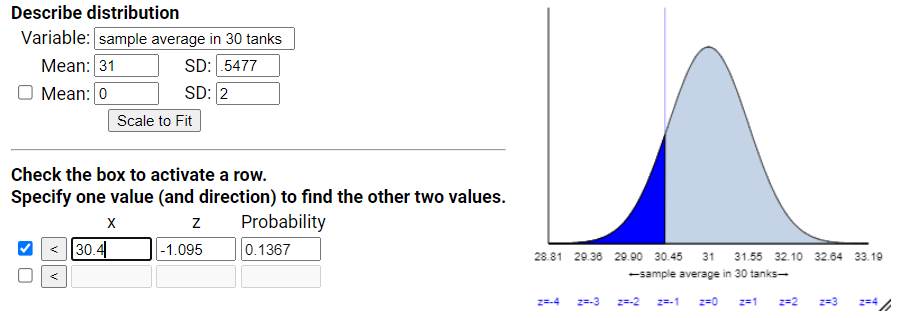
About
13.7% of random samples of 30 tanks will have an average mileage of 30.4 mpg by
random chance alone. We would probably
not consider this a surprising outcome (happens more than 10% of the time).
(c) Assess the
validity of your calculations in (a) and (b)
It’s
always reasonable to calculate a “standard score” as I did in (a). If I wanted to convert this z-value to a
probability, then I would need to know that the tank MPGs follow a normal
distribution. We aren’t told that here though it seems a reasonable assumption.
As stated in (b), we can use the CLT if
we continue to have this belief in the normality of the MPG values in general
or if it’s not too crazy behaving because then the sample of size 30 tells us
that the distribution of sample means should still be approximately
normal.
If
you go to the Sampling from a Finite Population applet and
check the box for Population Model, you can simulate drawing random samples
from a probability distribution rather than a finite population. When the
probability distribution is a normal distribution, everything works very well:
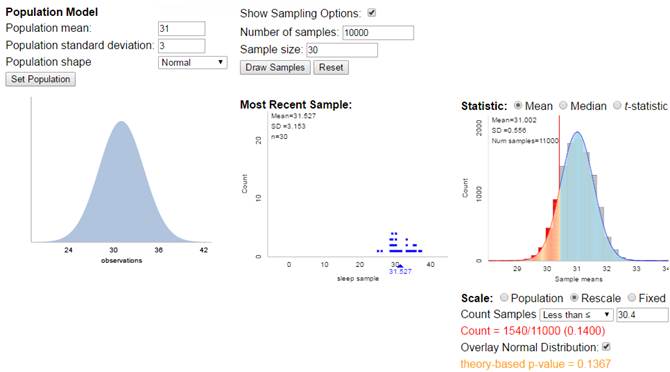
If
the theoretical probability distribution is not normal but symmetric, things
still work pretty well.
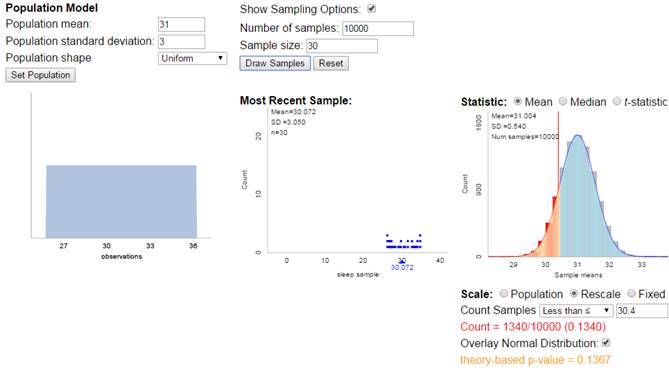
If
the theoretical probability distribution is not normal to begin with, things
still work pretty well due to the “large” sample size
3)
The file AgeGuesses.txt
contains students’ guesses of my age on the first day of class a few years ago.
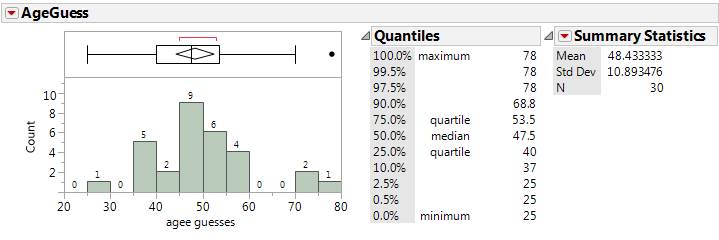
(a) Estimate and interpret a 95%
confidence interval for the population mean.
Confidence interval for the
population mean:
![]() + t*
(s /
+ t*
(s /![]() ) = 48.43 + t* (10.89/sqrt(30))
) = 48.43 + t* (10.89/sqrt(30))
For 95% confidence, we
estimate t* to be around 2.
48.42 + 2(1.99) =
(44.4, 52.4) years
I’m 95% confident that the
average guess of my age in the population of all Cal Poly students on such an
activity would be between 44.4 and 52.4 years
(More precisely, t* = 2.045)
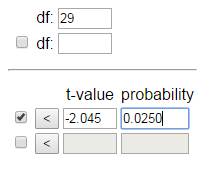
![]() + t*
(s /
+ t*
(s /![]() ) = 48.43 + 2.045 (10.89/sqrt(30))
= (44.36, 52.50). A little bit wider.
) = 48.43 + 2.045 (10.89/sqrt(30))
= (44.36, 52.50). A little bit wider.
On an exam without the computer, for 95% confidence you can use 2
for either z* or t*. That’s why I said “estimate”
(b) Estimate and interpret a 95%
confidence interval for the next student’s guess of my age.
![]() + t*
(s
+ t*
(s ![]() ) = 48.43 + 2 (10.89 × sqrt(1+1/30))
= (26.29, 70.6)
) = 48.43 + 2 (10.89 × sqrt(1+1/30))
= (26.29, 70.6)
I’m 95% confident that any one
Cal Poly student would guess my age between 26.3 and 70.6 years.
(More precisely)
![]() + t*
(s
+ t*
(s ![]() ) = 48.43 + 2.045 (10.89 × sqrt(1+1/30))
= (25.79, 71.07)
) = 48.43 + 2.045 (10.89 × sqrt(1+1/30))
= (25.79, 71.07)
(c) Which interval do you feel is more
meaningful in this context?
Opinions will vary, the
prediction interval is quite wide due to the huge amount of variation in the
responses given to this question. Typically a prediction interval is more meaningful (what
will happen next, vs. what is the long-run mean), but because it’s so wide this
one is not very informative, basically saying I went to graduate school but I’m
still alive!
(d) What information would you need to
know to decide whether students’ are “biased” in how
they guess my age? If you did a test of
significance, would this be a one-sided or a two-sided test?
You would need to know my
actual age, then we could see whether the sample mean fell above that
(overestimating my age on average) or below that (underestimating my age on
average).
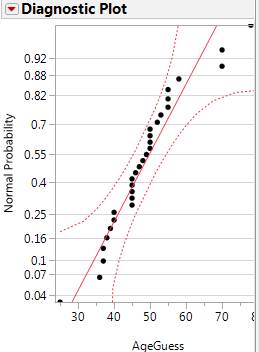
(e) Evaluate the validity of your
calculations in (a) and (b).
The distribution is pretty symmetric and the sample size is 30 so the confidence
interval in (a) is probably ok (achieves the stated 95% confidence in the long
run), but with the outliers on both sides, the sample distribution of age
guesses has heavier tails than we might expect for a normally distributed
population. If we believe these long tails exist in the population, then this
would cast some doubt as to the validity of the prediction interval (though
again, at least the distribution is symmetric, but there may be less than 95%
of the population distribution falling within 2 standard deviations of the
mean, or more if the population standard deviation is inflated by such
outliers). The nonlinear nature of the
normal probably plot suggests these data are not coming from a normally
distributed population.
(f) Column 2 indicates whether the data
were collected in Section 1 or Section 2.
I changed something about my appearance between the two sections.
Suppose I find a statistically significant difference in the average guess of
my age between the two classes, flipping a coin in advance to decide which
appearance I would use in each section. Would you be willing to attribute the
change in the ages to the change I made in my appearance? Explain why or why
not.
While I did randomly assign
the two treatments in a sense, I did so at the class level rather than at the
individual student level. So there could still be a confounding variable between the
two sections (e.g., I looked more tired later in the day) and we should not
draw any cause-and-effect conclusion here. (Actually
the average guess was 10 years larger in section 1!)
4)
In a recent study (Klein, Thomas, and Sutter, 2007), researchers found that
current smokers were more likely to have used candy cigarettes as children than
current nonsmokers were.
(a) Identify and classify the
explanatory and response variables.
EV = whether used candy cigarettes as child
RV = whether or not current smoker
(b) When first hearing of this study,
someone responded by saying, “Isn’t the smoking status of the parents a
confounding variable here?”
Explain
what “confounding variable” means in this context, and
describe how parents’ smoking status could be confounding (i.e., describe what
would need to be true).
It would be a confounding variable if it provides an alternative
explanation for the observed association. To do this, it must differ between
the explanatory variable groups and potentially impact the response
variable. So if
those with smoking parents are more likely to be allowed to play with candy
cigarettes as children but also more likely to smoke due to the environment
they were raised and/or genetics, then the smoking habits of the parents might
better predict who is a later smoker, but would also explain why current
smokers are more likely to have played with candy cigarettes.
5) Newspaper headlines proclaimed
that chocolate lovers live longer, following the publication of a study titled
“Life is Sweet: Candy Consumption and Longevity” in the British Medical
Journal (Lee and Paffenbarger, 1998). In 1988, researchers sent a health
questionnaire to men who entered Harvard University as undergraduates between
1916 and 1950. The study included 7841 men, free of cardiovascular disease and
cancer. From the questionnaire they determined whether the respondents consumed
candy “almost never” (3312 men) or “sometimes or often” (4529 men), and then
they tracked the participants to determine whether or not they had died by
1993.
(a) Identify
the observational units.
men
(b) Identify the
response variable.
Whether
or not the person had died by 1993.
(c) Identify
the explanatory variable.
Whether
the person was classified a candy consumer (sometimes or often) or not a candy
consumer (almost never)
(d) Was this an
experiment or an observational study? If an experiment, was it a randomized,
comparative experiment? If observational, was if a cohort, cross-classified, or
case-control study? This was an observational study
because the candy-consumption levels were not imposed on the men in the study, the men in the study chose for
themselves. This is probably best
classified as a cohort study because they were identified, their candy
consumption determined, and then followed for 5 years to determine the outcome
for the response variable. This means its legitimate for us to use this data to
estimate the probability of still being alive.
(e) Researchers
found that of respondents who admitted to consuming candy regularly, 267 had
died by the end of 1993, compared to 247 of the non-consumers of candy. Set up
the calculation for Fisher’s Exact Test for deciding whether candy consumers
are significantly less likely to have died than non-consumers by completing the
following:
Note:
The conditional proportions of death are 267/4529 = .05895 and 247/3312 =
.07458
Best
bet is to set up the two-way table:
|
|
candy
consumer |
non-consumer |
Total |
|
still
alive |
4262 |
3065 |
7327 |
|
Died |
267 |
247 |
514 |
|
Total |
4529 |
3312 |
7841 |
If we
let X represent the number still alive in the candy consumer group, then we
want to find above X (even more survivors in candy consumer group)
p-value = P(X
> 4262
) where X follows a hypergeometric distribution
with parameters
N
= 7841 M = 7327 n = 4529
We
can also look at the number deaths in the candy consumer group, which we expect
(in the long run) to be less than the number of deaths in the non-consumer
group. In this case, p-value = P(X < 267)
where X follows a hypergeometric distribution with parameters N = 7841, M = 514, and n = 4529.
(There
are other correct set ups as well.)
(f) Suppose you
wanted to carry out a simulation to determine how surprising it is for two
random samples from the same population to give a difference in sample proportions
at least this large. Describe the
simulation process (if describing an applet, name the applet and the input
information you would use).
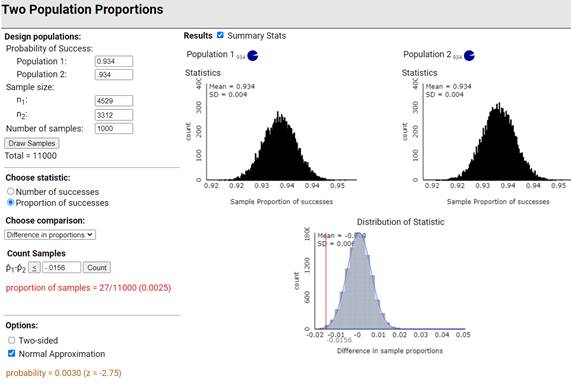
We
would randomly sample 4529 men and 3312 men, each from a population with a
probability of success of 7327/7841 = 0.934
Then
we would count how many samples have a difference as extreme (one-sided
alternative hypothesis) as 0.05895 – 0.07458 = -0.0156.
For
fun:
With
such large sample sizes, this is extremely statistically significant.
Also notice
that even though random sampling is probably a better model here, the FET
p-value is quite similar as well.
![]()
(g) The study
reported: Between 1988 and 1993, 514 men died: 7.5% of
non-consumers, but only 5.9% of consumers (age adjusted relative risk 0.83; 95%
confidence interval 0.70 to 0.98). Interpret
this statement as if to someone who has never taken a statistics class. In particular, what
do you think is meant by “age adjusted relative risk”?
This
interval provides an assessment for how much less likely a candy consumer is to
die in this time frame than a non-consumer. The values in the interval are all
less than one, so if we knew the death rate of non-consumers, we would multiply
by .70 to .98 to find the death rate for those who eat candy.
“Age
adjusted relative risk” essentially looks at the relative risks in different
ages groups (so only comparing men of similar ages) and then roughly averages
across those values to get an age-adjusted relative risk. This helps ensure we
have “controlled” for age since we couldn’t do random assignment.
(h) Based on
this interval, I would consider the comparison statistically significant. Why?
Yes,
because 1 is not inside this 95% confidence interval, we know the two-sided
p-value is less than .05.
(i) This does
not appear to be a large difference (7.5% vs. 5.9%), are you surprised that
this result is statistically significant? Explain.
1. No
because the relative risk takes the magnitudes of the values into account: 1.6
percentage points may not be a lot but it’s a decent fraction of 5.9%.
2.
The sample sizes are pretty large so even a weak
association will probably end up being “statistically significant.”
(j) The study
also reports: We then examined different levels of candy
intake. Compared with non-consumers, the relative risks of mortality among men
who consumed candy 1-3 times a month (1704 men), 1-2 times a week (1589 men),
and 3 or more times a week (1236 men) were 0.64 (0.48 to 0.86), 0.73 (0.55 to
0.96), and 0.84 (0.64 to 1.11),
Does this
result provide evidence of a “dose-response”? Explain.
Yes,
the relative “risk” of surviving that long is increasing with increasing
amounts of candy!
(k) And then: Finally, using life table analysis
truncated at age 95, we estimated that (after adjustment for age and cigarette
smoking) candy consumers enjoyed, on average, 0.92 (0.04 to 1.80) added years
of life, up to age 95, compared with non-consumers.
Based on these
results, are you willing to conclude that eat candy leads to a longer life?
No,
this was not a randomized comparative experiment, so we can’t draw any
cause-and-effect conclusions.
A
possible confounding variable is “happiness” – those who are happy and relaxed
and not worried about what they eat are more likely to consume candy than those
who are stressed and worried and watching their diet closely. But that happier lifestyle may also be
responsible for longer lives.
(l) What population
are you willing to generalize these results to? Explain.
At
most well-off males (graduates from Harvard), but even that is risky as this
study did not involve random sampling. It’s possible the access to medical care
and long-life span for such individuals is not representative of all adults
(certainly not women).
6) A study of whether AZT
helps to reduce transmission of AIDS from mother to baby (Connor et al., 1994):
Of the 180 babies whose mothers had been randomly assigned to receive AZT, 13 babies
were HIV-infected, compared to 40 of the 183 babies in the placebo group.
(a) Create a segmented bar graph to display
these results. Comment on what the graph reveals.
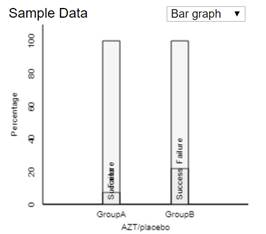
This
bar graph (and the conditional proportions of 13/180 vs. 40/183) indicates that
mothers given the placebo were about 3 times as more likely to have babies that
were HIV positive than were the mothers given AZT.
(b) Check the validity conditions for whether a
two-sample z-test can be applied to these data. Be sure to mention
whether the study involves random sampling from populations or random
assignment to treatment groups.
The number of
successes and failures in each group should be at least 5. The four
values are 13, 180-13 = 167, 40, 183-40=143. This condition is met.
(c) If you were to carry out a simulation to
obtain a p-value, would you simulate random sampling or random assignment? Explain.
The data are
from randomly assigning subjects to two treatment groups. So our p-value will want to reflect the random variation
from random assignment (e.g., shuffling the 363 cards (53 successes and 310
failures) to groups of 180 and 183).
(d) Conduct an appropriate test of significance
to determine whether the data provide convincing evidence that AZT is more
effective than a placebo for reducing mother-to-infant transmission of AIDS.
Report the hypotheses, test statistic, and p-value. Also indicate the test
decision using .01 as the level of significance.
The null
hypothesis is that AZT and a placebo are equally effective in reducing
mother-to-infant transmission of AIDS. Specifically, the probability of
HIV-positive babies born to mothers who could potentially take AZT is the same
as the probability of HIV-positive babies born to mothers who could potentially
take a placebo. In symbols, the null hypothesis is H0: πAZT
- πplacebo = 0.
The
alternative hypothesis is that AZT is more effective than a placebo for
reducing mother-to-infant transmission of AIDS, or that the probability of
HIV-positive babies born to mothers who could potentially take AZT is smaller
than the probability of HIV-positive babies born to mothers who could
potentially take a placebo. In symbols, the alternative hypothesis is Ha:
πAZT - πplacebo < 0.
Because this
is a randomized experiment and the counts are on the small size, we could carry
out Fisher’s Exact Test.

Or we could
carry out the random assignment simulation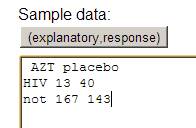
And find the
p-value by counting how many re-random assignments have a difference in
proportion with HIV positive babies (![]() AZT –
AZT – ![]() placebo) of -.146 or less
placebo) of -.146 or less
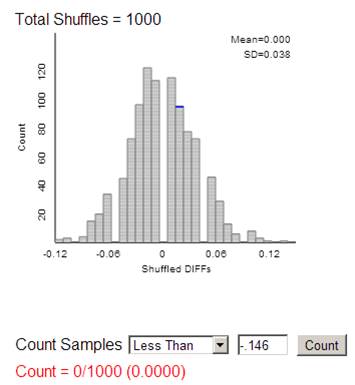
Or, because
we said in (b) that the theory-based approach should be valid, we could go
straight to the Theory-Based applet to carry out a ‘two-sample z-test’
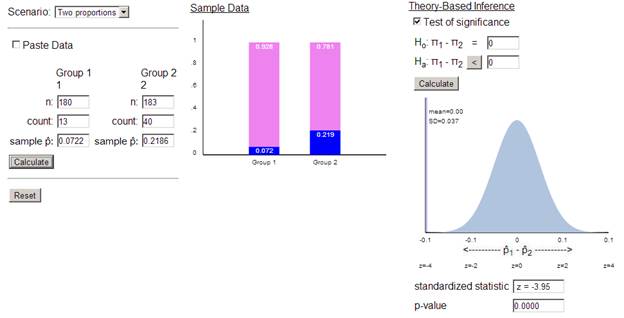
With such a
small p-value, reject H0 at the .01 level of significance.
We have very
strong statistical evidence that AZT is more effective than a placebo for
reducing mother-to-infant transmission of AIDS. We can say ‘more effective”
because this was a randomized, comparative experiment.
(e) Estimate the relative risk of transmission
with the placebo compared to AZT with a 95% confidence interval. Also be sure
to interpret this interval in context.
Sample
relative risk (with placebo in numerator): (40/183)/ (13/180) = 3.03
For 95%
confidence, z* = 1.96
For relative
risk, we first take the ln rel risk: ln(3.03) = 1.106
SE(ln rel risk)
= sqrt(1/40 – 1/183 + 1/13 – 1/180) = 0.3015
Confidence
interval: 1.106 + 1.96(.3015) = (0.515, 1.697)
Back-transforming:
exp(0.515, 1.697) = (1.67, 5.46)
We are 95%
confident that the probability of transmission is 1.67 to 5.46 times higher
with the placebo than with AZT.
(f) Summarize the conclusion that you could draw
from this study (significance, estimation, causation, and generalizability).
Also explain the reasoning behind each component.
Because
this was a well-designed experiment with a small p-value, we can
conclude that AZT caused the observed difference in HIV transmission
rates. If AZT and a placebo were equally effective in reducing
mother-to-infant transmission of AIDS, we virtually never see sample results as
or more extreme as those we saw in this experiment by random assignment alone
(p-value < .0001). We are 95% confident that using the placebo increases the
probability of transmission by 67% to 546%. We might have some caution in
generalizing these results to a larger population as we don’t know how the
HIV-positive mothers willing to participate in this study were recruited.
7) Consider the question of whether exposure to second-hand smoke is
harmful to the health of children. EV = whether or not
exposed to second hand smoke, RV = health of child
(a) Describe a prospective
cohort observational study that could address this question.
Find children who will be
exposed to second hand smoke and children who
won’t. In a few years, compare the health of the two groups.
(b) Describe a retrospective
case-control observational study that could address this question.
Find healthy children and unhealthy children and then see how much
second-hand smoke they were exposed to growing up.
(c) Describe a cross-classified
observational study that could address this question.
Find older children and
then determine their health status and whether they were exposed to different
amount of second-hand smoke.
(d) Describe how you could (in
principle) design an experiment to address this question.
Randomly assign some
children to be exposed to second-hand smoke and some children not to be exposed
to second-hand smoke.
(e) Would it be ethical to
conduct an experiment to address this question? Explain.
Because second-hand smoke
is so potentially hazardous, it would not be ethical to willing impose this
treatment on children.
8)
Investigation 3.10
(a) The observational units are drivers;
Explanatory variable is whether or not got a full
night’s sleep in previous week; Response variable is whether or not were
involved in a car crash; This is a case-control observational study.
(b)
|
|
No full night’s sleep |
Full night’s sleep |
Total |
|
Crash |
61 |
535-61 = 474 |
535 |
|
No Crash |
44 |
588 – 44 = 544 |
588 |
|
Total |
105 |
1018 |
1123 |
(c) Because this was a case-control study
we should use the odds ratio. If we look at the odds of being in a crash if
they did not get a full night’s sleep compared to the odds of being in a crash
if they did get a full night’s sleep: (61/44)/(474/544)
= 1.5911
Note,
this is the same as the odds of not getting a full night’s sleep for the crash
victims vs. the odds of not getting a full night’s sleep for the non-crash
subjects.
The
odds of being in a crash if didn’t get a full night’s sleep were 1.59 times
higher than the odds of being in a crash if did get at least one full night’s
sleep.
(d) We could replicate the sampling
design by sampling independently from two binomial processes with the same
probability of success (this will model H0: ![]() = 1). One
process will represent the sampling of the crash victims (n = 535) and the other will represent the sampling of the no-crash
population (n = 588). We can use 105/1123 » 0.581 as the common probability of
success. Once we get the two samples, we
will calculate the simulated odds ratio.
Then we will see how often we get a sample odds ratio of 1.5911 or
larger (Ha:
= 1). One
process will represent the sampling of the crash victims (n = 535) and the other will represent the sampling of the no-crash
population (n = 588). We can use 105/1123 » 0.581 as the common probability of
success. Once we get the two samples, we
will calculate the simulated odds ratio.
Then we will see how often we get a sample odds ratio of 1.5911 or
larger (Ha: ![]() > 1,
note, it’s not clear here whether they had a one or two sided alternative in
mind, but it’s reasonable to think that they suspected the lack of sleep would
be associated with an increase in odds of a car crash.).
> 1,
note, it’s not clear here whether they had a one or two sided alternative in
mind, but it’s reasonable to think that they suspected the lack of sleep would
be associated with an increase in odds of a car crash.).
(e) Let Xcrash be the number
of successes (no full night’s sleep) in the crash group, so we are modeling Xcrash
as binomial with n = 535 and ![]() =
0.0935.
=
0.0935.
Let
Xno crash be the number of successes in the “no crash” group, and
we are modeling Xno crash as binomial with n = 588 and p = 0.0935.
Then
odds ratio = (Xcrash/Xno crash) / [(535 - Xcrash)/(588
- Xno crash)]
The
distribution should appear skewed to the right with mean close to 1 and
standard deviation near 0.2.
Example
results:
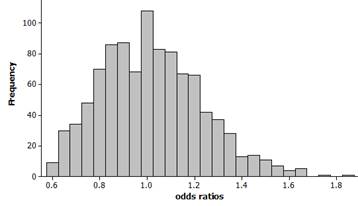
mean
= 1.108, standard deviation = 0.2129
The
observed ratio of 1.59 is a fair bit out in the tail of the distribution and
appears to have a smallish p-value. If we
count how many of these observations are 1.59 are larger (rounding down from
1.5911 so that 1.5911 is included), we find about 1% (10 out of 1000) of the
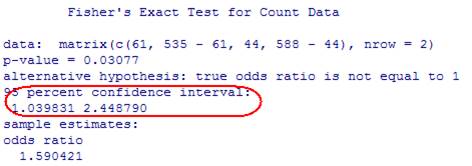
simulated sample odds ratios are at least this extreme. Using Fisher's Exact test, the p-value is 0.0158 = P(X
≥ 61, for X hypergeometric with N
= 1123, M = 535, n = 105. This
gives us strong evidence, of a relationship in the population.
(f) Theoretical
standard error for the log odds ratio:
![]() »
0.2075
»
0.2075
ln(1.59) + 1.96(0.2075) = 0.4637 + 0.4067 Þ (0.057, 0.870)
exp(0.057, 0.070) Þ (1.06, 2.39)
We
are 95% confident that the odds of being in a car crash are 1.06 to 2.39 times
larger for those without a full night’s sleep in the previous week compared to
those with at least on full night’s sleep.
This
interval does not capture one, so we have statistically significant evidence of
an increase in odds for those without a full night’s sleep.
R output (R inverts a test (doubling the
one-sided p-value) rather than using the z-formula)
JMP output
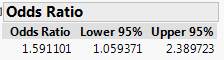
These
are very close to the confidence interval we calculated.
(g) We have
strong evidence (p-value = 0.0158) that sleep deprived drivers have higher odds
(4% to 140% higher) of being in a car crash, at least for drivers like these
New Zealand drivers. We cannot draw a cause-and-effect conclusion however as
this was an observational study. We
should probably apply these results only to drivers in New Zealand at that
time.