Stat 301 – Review 2
Problems
1) (~5 pts) Weights of 30 (fun-size) Mounds candy bars and 20 (fun-size) PayDay candy bars, in grams, are shown
in the dotplots below.
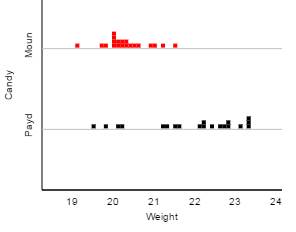
Explain your
answers to the following:
(a) Which
distribution would you consider skewed to the right?
(b) Which
distribution do you expect has a larger mean?
(c) Which
distribution do you expect has a larger standard deviation?
(d) Which
distribution would you suspect will have its mean larger than its median?
2) (~8 pts) The highway miles per
gallon rating of the 1999 Volkswagen Passat was 31 mpg (Consumer Reports,
1999). The fuel efficiency that a driver obtains on an individual tank of
gasoline naturally varies from tankful to tankful. Suppose the mpg calculations
per tank of gas have a (long-run) mean of ![]() = 31 mpg and a standard deviation of
= 31 mpg and a standard deviation of ![]() = 3 mpg.
= 3 mpg.
(a) Would it be
surprising to obtain 30.4 mpg on one tank of gas? Explain.
(b) Would it be surprising for a sample of 30
tanks of gas to produce a sample mean of 30.4 mpg or less? Explain, referring
to the CLT and to a sketch that you draw of the sampling distribution.
(c) Assess the
validity of your calculations in (a) and (b).
3) (~15 pts) The file AgeGuesses.txt
contains students’ guesses of my age on the first day of class a few years ago.
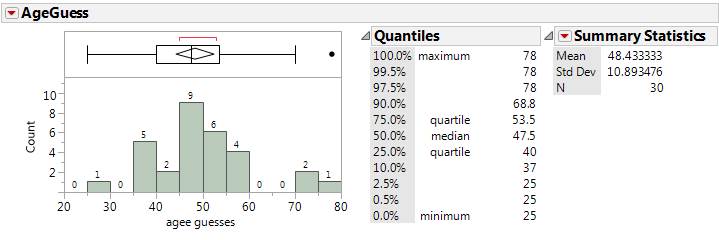
(a) Estimate and interpret a 95%
confidence interval for the population mean.
(b) Estimate and interpret a 95%
confidence interval for the next student’s guess of my age.
(c) Which interval do you feel is more
meaningful in this context? Explain your reasoning.
(d) What information would you need to
know to decide whether, in the long-run, students are “biased” in how they
guess my age? If you did a test of
significance, would this be a one-sided or a two-sided test?
(e) Evaluate the validity of your
calculations in (a) and (b).
(g) Column 2 of the AgeGuesses data file
indicates whether the data were collected in Section 1 or Section 2. I changed something about my appearance
between the two sections, flipping a coin in advance to decide which appearance
I would use in each section. Suppose I find a statistically significant
difference in the average guess of my age between the two classes. Would you be
willing to attribute the change in the ages to the change I made in my
appearance? Explain why or why not.
4)
(~ 7 pts) In a recent study (Klein, Thomas, and Sutter, 2007),
researchers found that current smokers were more likely to have used candy
cigarettes as children than current nonsmokers were.
(a) Identify and classify the
explanatory and response variables.
(b) When first hearing of this study,
someone responded by saying, “Isn’t the smoking status of the parents a
confounding variable here?” Explain what “confounding variable” means in this
context, and describe how parents’ smoking status could be confounding (i.e.,
describe what would need to be true).
5) (~ 20 pts) Newspaper headlines proclaimed
that chocolate lovers live longer, following the publication of a study titled
“Life is Sweet: Candy Consumption and Longevity” in the British Medical
Journal (Lee and Paffenbarger, 1998). In 1988, researchers sent a health
questionnaire to men who entered Harvard University as undergraduates between
1916 and 1950. The study included 7841 men, free of cardiovascular disease and
cancer. From the questionnaire they determined whether the respondents consumed
candy “almost never” (3312 men) or “sometimes or often” (4529 men), and then
they tracked the participants to determine whether or not they had died by
1993.
(a) Identify
the observational units.
(b) Identify
the response variable.
(c) Identify
the explanatory variable.
(d) Was this an
experiment or an observational study? If an experiment, was it a randomized,
comparative experiment? If observational, was it a cohort, cross-classified, or
case-control study?
(e) Researchers
found that of respondents who admitted to consuming candy regularly, 267 had
died by the end of 1993, compared to 247 of the non-consumers of candy. Set up
the calculation for Fisher’s Exact Test for deciding whether candy consumers
are significantly less likely to have died than non-consumers by completing the
following:
p-value = P(X ) where X follows a distribution with parameters
N
= M = n =
(f) Suppose you
wanted to carry out a simulation to determine how surprising it is for two
random samples from the same population to give a difference in sample proportions
at least this large. Describe the
simulation process (if describing an applet, name the applet and the input
information you would use).
(g) The study
reported: “Between 1988 and 1993, 514 men died: 7.5%
of non-consumers, but only 5.9% of consumers (age adjusted relative risk 0.83;
95% confidence interval 0.70 to 0.98).” Interpret
this statement as if to someone who has never taken a statistics class.
Extra credit:
What do you think is meant by “age adjusted relative risk”?
(h) Based on
this interval, I would consider the comparison statistically significant. Why?
(i) This does
not appear to be a large difference (7.5% vs. 5.9%), are you surprised that
this result is statistically significant? Explain.
(j) The
study also reports: We then examined different levels of candy
intake. Compared with non-consumers, the relative risks of mortality among men
who consumed candy 1-3 times a month (1704 men), 1-2 times a week (1589 men),
and 3 or more times a week (1236 men) were 0.64 (0.48 to 0.86), 0.73 (0.55 to
0.96), and 0.84 (0.64 to 1.11),
Does this
result provide evidence of a “dose-response”? Explain.
(k) And then: “Finally, using life table analysis
truncated at age 95, we estimated that (after adjustment for age and cigarette
smoking) candy consumers enjoyed, on average, 0.92 (0.04 to 1.80) added years
of life, up to age 95, compared with non-consumers.“ Based on these results, are you willing
to conclude that eat candy leads to a longer life?
(l) To what
population are you willing to generalize these results? Explain.
6) (~ 20 pts) A
study of whether AZT helps to reduce transmission of AIDS from mother to baby
(Connor et al., 1994): Of the 180 babies whose mothers had been randomly
assigned to receive AZT, 13 babies were HIV-infected, compared to 40 of the 183
babies in the placebo group.
(a) Create a segmented bar graph to display
these results. Comment on what the graph reveals.
(b) Check the validity conditions for whether a
two-sample z-test can be applied to these data.
(c) If you were to carry out a simulation to
obtain a p-value, would you simulate random sampling or random assignment? Explain.
(d) Conduct an appropriate test of significance
to determine whether the data provide convincing evidence that AZT is more
effective than a placebo for reducing mother-to-infant transmission of AIDS.
Report the hypotheses, test statistic, and p-value. Also indicate the test
decision using .01 as the level of significance.
(e) Estimate the relative risk of transmission
with the placebo compared to AZT with a 95% confidence interval. Also be sure
to interpret this interval in context.
(f) Summarize the conclusion that you could draw
from this study (significance, estimation, causation, and generalizability).
Also explain the reasoning behind each component.
7)
(~10 pts) Consider the question of whether exposure to
second-hand smoke is harmful to the health of children.
(a) Describe a prospective
cohort observational study that could address this question.
(b) Describe a retrospective
case-control observational study that could address this question.
(c) Describe a cross-classified
observational study that could address this question.
(d) Describe how you could (in principle)
design an experiment to address this question.
(e) Would it be ethical to
conduct an experiment to address this question? Explain.
8) Investigation 3.10
See also Examples 2.1, 3.1, 3.2