Stat 301 – HW 3

Due midnight, Friday, Jan. 26

Please remember to put your name(s) inside the file and if submitting jointly to join a HW 3 group first. Please use Word or PDF format only. Remember to integrate your output with your discussion. Points will be deducted if you are missing output.

1) Finish your water journal and submit your results by Feb. 2. Include your answers to (a)-(e) now.

After the 7 days, open the water use survey (you will need to make a copy first) and complete rows 2-15 (and indicate CA for the state you live in). Be sure to make any conversions you need before entering your values in column D (e.g., average per day, number per year).. Everyone will leave rows 16-20 blank. When you have completed your journal, use the “Water Survey” link in Canvas to::

(a) Upload a copy of your journal

(b) Report your Total (Individual Daily Use) from cell F21.

Then also answer:

(c) Report any suspected data quality errors.

(d) Suppose we find the average water usage (find the mean of all your answers to b), will this be a parameter or a statistic? Then define in words a corresponding statistic/parameter.

(e) Suggest a research question you could explore using one of these variables.

2) Hill and Barton (Nature, 2005) conducted a study to investigate whether Olympic athletes in certain uniform colors have an advantage over their competitors. They noted that competitors in the combat sports of boxing, tae kwon do, Greco-Roman wrestling, and freestyle wrestling are randomly assigned to wear red or blue uniforms. For each match in the 2004 Olympics, they recorded the uniform color of the winner. They found that in 457 Olympic combat sport matches, the competitor wearing red won 248 times (successes), while the person wearing blue won 209 times (failures).

(a) Identify the observational units and variable of interest in this study.

(b) Define the parameter in words (in context).

(c) State appropriate null and alternative hypotheses in symbols and/or words.

(d) Report the sample proportion, .

(e) Is the normal approximation to the binomial distribution likely to be valid for this study? Explain how you are deciding.

(f) Find both the exact binomial p-value and the p-value from the one-sample z-test using R or the One Proportion Inference applet. (Include a copy of the distributions overlaid.) Are they similar? Does the similarity/lack of similarity of these values surprise you? Explain.

(g) Report and interpret, in context, the standardized statistic from (f).

(h) The continuity correction is discussed in Investigation 1.8. Use R or the applet to perform a continuity correction for the calculations in (f). Does this continuity correction improve the normal approximation of the exact binomial calculation for this situation? (Make sure you are including sufficient output.)

(i) Below is the exact binomial confidence interval from R

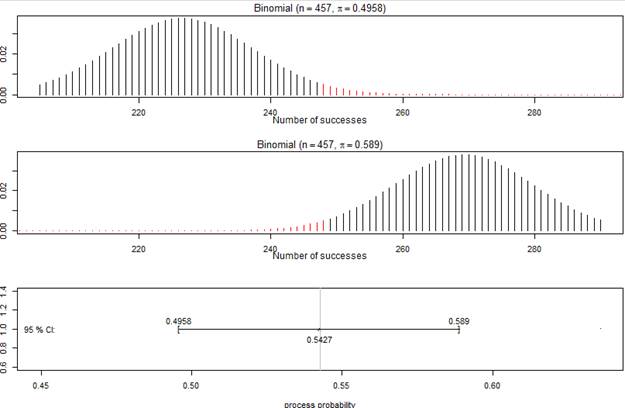
Interpret the interval in context.

(j) Are the confidence interval and binomial p-value consistent with each other? Explain how you are deciding.

(k) Use R or the Theory-Based Inference applet to find a 95% z-confidence interval. Are the z-interval and exact binomial confidence intervals similar? Is this what you would expect for these data? Explain.

(l) The adjusted-Wald confidence interval procedure is discussed in Investigation 1.9. The procedure is to add two successes and two failures to the sample before computing the z-confidence interval. Use technology to find the 95% adjusted-Wald confidence interval. Make sure it’s clear how you are doing so.

(m) Compare the widths of the three confidence intervals you have found. (Use 4 decimal places.) Which is the shortest?

(n) Report the half-width (aka margin of error) for the one-proportion z-confidence interval in (k). Compare this value to . Based on the formula for the margin of error in the 95% one-proportion z-confidence interval, why does this approximation make sense?

(o) So a short-cut approximation to the one-proportion z-confidence interval is . If anything, this interval will be wider than it needs to be (is “conservative”). Why? (Hint: How does the standard error formula change with ?)

Keep in mind

· In this class, we will use the term standard error to refer to an estimate of the standard deviation of the statistic (computed entire from information available in the sample data). Interpret a standard error just like you would the standard deviation of the statistic (e.g., a typical deviation of the statistic from the parameter across different samples).

· If I don’t give you a confidence level, assume 95%.