Stat 301 – Final Exam Review Solutions
1. Recall from
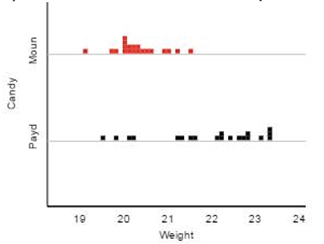
the exam 2 review problems the weights of 30 (fun-size) Mounds candy bars and 20 (fun-size) PayDay candy bars, in grams.
(e) State null and
alternative hypothesis for comparing the means of these two distributions, both
in symbols and in words.
Let 
represent the
long-run mean weight for the Mounds manufacturing process and 
the
long-run mean weight for the PayDay manufacturing process. We
want to know whether the observed difference in these sample means convinces us
that there is a genuine difference in the long-run mean weights for these two
manufacturing processes.
H0: - = 0 (no difference
in the long-run means)
Ha: - ≠ 0
(this is a difference in the long-run means)
We were
just asked to compare the means, there was no prior suspicion given as to which
candy bars would be heavier, so we are using a two-sided alternative.
(f) Do you
think a theory-based analysis would be appropriate for these data? Explain how
you are deciding.
It’s a little questionable, the sample sizes are
both at least 20 but we do have some skewness in the sample distributions (and
in opposite directions). Would probably be worth looking at a second
analysis as well.
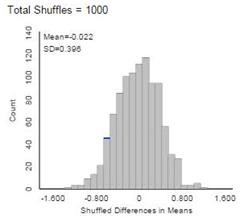
(g) Is this
distribution approximately normal? Would you have expected this? Explain
This distribution looks a bit skewed left,
consistent with our skepticism in question (f).
(h) Would you
expect this distribution to follow a t distribution? Explain
Actually, the t probability
distribution model is for the standardized statistics, not the distribution of
the differences in sample means. We don’t quite see the heaviness in the tails
(because we aren’t using the s’s yet) that we might for
the t distribution.
(i) Use the
above output to roughly approximate the p-value. Explain how.
First
we have to roughly approximate the difference in sample means from the original dotplots,
keeping in mind that the PayDay mean might be pulled a little bit to
the left of the main peak. Maybe 22.2 grams and 20.5 grams?? So say
we think the difference in means is around 2 grams. Then we need to
look at the randomization distribution and see how often we get a difference of
-2 or smaller or a difference of 2 or larger for a two-sided
p-value. However, we see 2 is off the chart on both ends so this
would approximate a p-value of zero. In
reality the difference in means is 1.605 grams, which is still pretty extreme
and the empirical p-value is zero.
(j) Explain a
difficulty with using this simulation approach to analyze these data.
This is a randomization distribution, assuming
random shuffling of the weights to the two brands. But that is not how the
data were collected, that was through independent random sampling from each
random process. So we might prefer a simulation that reflects the
randomness from sampling from an infinite process rather than from random
assignment (this distribution would also center at zero but would likely have a
bit different standard deviation).
(k) Assuming
it’s valid, how would you interpret this confidence interval?
I’m 95% confident that the mean weight of
(all) PayDay candy bars is 0.99 to 2.22 grams larger than the mean
weight of (all) Mounds candy bars.
2) A study
examined whether a nicotine lozenge can help a smoker to quit. The research
reports on many background variables, such as age, weight, gender, number of
cigarettes smoked, and whether the person made
a previous attempt to quit smoking (Shiffman et al., 2002). Suppose the
researchers want to compare the distributions of the background variables
between the two treatment groups (nicotine lozenge or placebo lozenge).
(a) For each of the five variables listed,
indicate whether it calls for a comparison of means or a comparison of
proportions.
Age –
quantitative – means
Weight
– quantitative – means
Gender
– categorical – proportions
Number
of cigs smoked – quantitative - means
Previous
attempt – categorical – proportions
(b) Would the researchers hope to reject the
null hypotheses or fail to reject the null hypotheses in these tests? Explain.
In this case, large p-values would be good news –
it would provide more evidence that our treatment groups were similar to each
other at the beginning of the study so any differences observed at the end of
the study are even more safely attributed to the nicotine lozenge’s superior
effectiveness to the placebo lozenge.
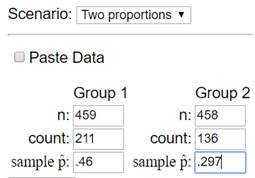
(c) Of the 459 nicotine users, 46.0% successfully abstained (didn’t
start smoking again) for 6 weeks, compared to 29.7% of the 458 control group
(without nicotine). Calculate and interpret a 95% confidence interval.
This
would be a “two sample proportions z-interval”
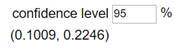
I’m
95% confident that, in the population of smokers like these (see demographics),
the probability of abstaining is .1009 to .2246 larger when assigned to
nicotine rather than to the placebo.
(d)
Are you willing to draw a cause-and-effect conclusion from this study? If not,
suggest a possible confounding variable and explain how it is confounding in
this study.
Yes,
because there was random assignment to the treatment groups (nicotine or not)
and the confidence interval does not contain zero (indicating a small p-value,
rejecting the null hypothesis of no difference in the probability of quitting between
the two treatments).
(e)
Are you willing to generalize these results to all smokers interested in
quitting? If not, suggest a possible source of sampling bias and the likely
direction of the bias.
Maybe
not, we don’t have a lot of information about how these individuals were
recruited. Maybe those willing to
participate in a smoking cessation study are different (more likely to abstain)
than those who want to quite but aren’t willing to participate in a research study.
3) Researchers examined the long-term survival
of doctors graduating from one medical school over one century
(Redelmeier and Kwong, 2004), comparing those who were presidents of
their class to those who appeared alphabetically before or alphabetically after
the president in the graduating class photograph. Statistics on
long-term mortality were obtained from licensing authorities, medical
obituaries, professional associations, alumni records, and national physician
directories (follow-up 94%). They reported on 507 presidents and
1014 classmates.
(a) Is it reasonable to treat
the presidents and non-presidents as independent random samples?
This
is a bit debatable, because they took all three individuals from the same year,
rather than taking a random sample of presidents and then a separate random
sample of non presidents. But if we
don’t think the variable changes too much from year to year, and there is no
real “connection” between adjusted records in the yearbook, we could treat them
as independent samples of presidents and non-presidents. It might be better to
more directly compare the 3 classmates from each graduating class, but it’s not
obvious how to do that either. It’s not clear how the 507 were selected or whether
that is all of the presidents. This is
also from just one school.
Assuming the answer to (a)
is yes:
(b) The researchers examined
several base-line variables, including gender and whether or not the individual
wore glasses. They found 93% of the presidents were male, compared
to 85% of their classmates. They also found 9% of presidents were
glasses, compare to 12% of their classmates. Are either of these
differences statistically significant?
Because the response variables
here (sex and whether wore glasses) are categorical, we will consider the
two-sample z procedure. In both cases, we can define 
- 
as the parameter of interest and then test
hypotheses H0: - = 0 (no difference in the population
proportions) vs. Ha: - ≠ 0 (there is a difference in the
population proportions). Because the sample sizes are large, the two-sample z-procedures
are likely valid.
JMP output for male/female
comparison:
There is a statistically
significant difference (p-value <.001 < .05) in the sample proportion of
presidents who were male compared to the sample proportion of classmates who
were male. We are 95% confident that the population proportion of all classmates
who are male is .05 to .11 lower than the population proportion of all presidents
who are male.
Applet and JMP output for
glasses comparison:
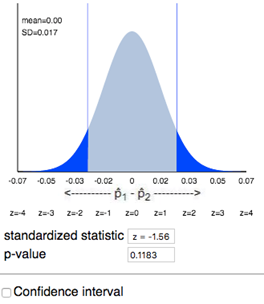
There is not a statistically
significant difference (p-value = .1187 > 0.05) in the proportion wearing
glasses.
(c) The overall-life
expectancy for the presidents was 49.0 years compared to 51.4 years for their
classmates. The two-sided p-value was reported to be
.036. Assuming the sample standard deviations were similar in the
two samples, use trial-and-error in JMP or TBI applet or algebra to approximate
the value of this standard deviation. What conclusion would you draw
from this p-value?
Let 
represent the life-expectancy
(mean lifetime) for all class presidents and 
represent the life-expectancy
for all classmates.
H0: 
= 0 (no difference in the average
life-expectancy between these two populations)
Ha: (there is a difference)
If we use the conservative df
of 506, a two-sided p-value of .036 corresponds to t0 = -2.102.
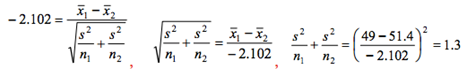
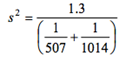=439.4, so s = 20.96.
The sample standard deviation must have been close
to 21 years.
Using this value below to verify the p-value:
The
p-value of .036 provides moderate evidence (.01 < p-value < .05) of a
difference between the population mean life expectancy of the class presidents
compared to their classmates. We would reject the null hypothesis at the 5%
level.
4) Because these were two different questions on the same survey, each
respondent is answering both questions, we shouldn’t apply a “two-sample”
procedure, but should treat the observations as paired instead.
5) In a study reported in the July 6, 2007 issue
of the journal Science, researchers studied 396 American college
students and kept track of each student’s sex and also how many words they
spoke in a day. They found that females spoke an average of 16,215 words per
day and males an average of 15,669 words per day.
Consider
the following variables:
- Sex
- Average number of words spoken per
day
- Number of adjectives used per day
- Proportion of words
spoken in a day by each student that were adjectives
- Whether more than 15,000 words were spoken
For each
research question below, which theory-based method would you consider:
·
One-proportion z-test or
interval
·
One-mean t-test or
interval
·
Two-proportion z-test or
interval
·
Two-mean t-test or
interval
Briefly justify your answer.
(a) Do women tend to use more words than men?
Two-mean t-test
(b) How often does the proportion of
adjectives a person uses in a day exceed 0.25? In other words, estimate the
probability more than 25% of the words someone uses in a day are adjectives.
Confidence interval for one proportion (variable: whether or not
exceed .25; parameter: probability of exceeded 0.25.)
(c) Are women more likely than men to use more than 15,000 words
per day?
Two-proportion z-test
(d) Do people tend to talk more (use more words) on the weekends
or on the weekdays?
Paired t-test (difference in number of words) or one proportion
(probability of using more on weekend than weekday). We are measuring the sample person on
weekends and on weekdays, so we could either calculate the difference in the
number of words or count how many times they talked more on the weekends as our
variable.
6)The Roller Coaster Database
maintains a web site (www.rcdb.com) with
data on roller coasters around the world. Some of the data recorded
include whether the coaster is made of wood or steel and the maximum speed
achieved by the coaster, in miles per hour. The boxplots display the
distributions of speed by type of coaster for 145 coasters in the United
States as of Nov. 2003.
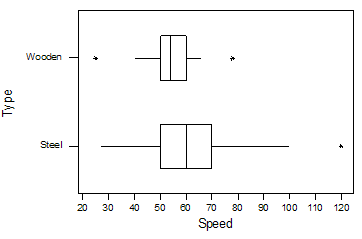
(a)
Do these boxplots allow you to determine whether there are more wooden or steel
roller coasters?
No,
no sample size information presented
(b)
Do these boxplots allow you to say which type has a higher percentage of
coasters that go faster than 60mph? Explain and, if so, answer the
question.
50%
of steel go faster than 60 mph compared to 25% of wooden
(c)
Do these boxplots allow you to say which type has a higher percentage of
coasters that go faster than 50mph? Explain and, if so, answer the
question.
Both
types have 75% exceeding 50 mph.
(d)
Do these boxplots allow you to say which type has a higher percentage of
coasters that go faster than 48mph? Explain and, if so, answer the
question.
No,
because 48 mph does not match up with a quartile, we can’t say anything about
how the values compare to 48mph. We know nothing about how the lowest 25% are
distributed along those “whiskers.” In
particular, having longer whiskers doesn’t imply a higher percentage in that
area.
(e)
The steel coasters have a “high outlier.” Explain how I know this from the
above display and interpret this outlier in context. What would be your next
step in analyzing these data?
The
star plotted off on its own. This is a
coaster than goes much faster than all the rest. We should figure out which coaster it is. We
can also see how the distribution changes if that observation is removed.
(f)
Conjecture as to how the mean, median, interquartile range, and standard
deviation will change (if at all) if that coaster identified in part (e) (Top
Thrill Dragster in Cedar Point Amusement Park, Sandusky, Ohio) is removed from
the data set. Explain your reasoning.
Removing
a high outlier will lower the mean and even the median, but probably more
noticeably for the mean.
Removing
a high outlier that is far from the mean will lower the variability in the data
so the interquartile range and standard deviation will decrease, but probably
more noticeably for the standard deviation.